Parabola

Parabola

The parabola is a member of the family of conic sections.
In mathematics, a parabola is a plane curve which is mirror-symmetrical and is approximately U shaped. It fits several other superficially different mathematical descriptions, which can all be proved to define exactly the same curves.
One description of a parabola involves a point (the focus) and a line (the directrix). The focus does not lie on the directrix. The parabola is the locus of points in that plane that are equidistant from both the directrix and the focus. Another description of a parabola is as a conic section, created from the intersection of a right circular conical surface and a plane which is parallel to another plane that is tangential to the conical surface.[1]
The line perpendicular to the directrix and passing through the focus (that is, the line that splits the parabola through the middle) is called the "axis of symmetry". The point on the parabola that intersects the axis of symmetry is called the "vertex", and is the point where the parabola is most sharply curved. The distance between the vertex and the focus, measured along the axis of symmetry, is the "focal length". The "latus rectum" is the chord of the parabola which is parallel to the directrix and passes through the focus. Parabolas can open up, down, left, right, or in some other arbitrary direction. Any parabola can be repositioned and rescaled to fit exactly on any other parabola—that is, all parabolas are geometrically similar.
Parabolas have the property that, if they are made of material that reflects light, then light which travels parallel to the axis of symmetry of a parabola and strikes its concave side is reflected to its focus, regardless of where on the parabola the reflection occurs. Conversely, light that originates from a point source at the focus is reflected into a parallel ("collimated") beam, leaving the parabola parallel to the axis of symmetry. The same effects occur with sound and other forms of energy. This reflective property is the basis of many practical uses of parabolas.
The parabola has many important applications, from a parabolic antenna or parabolic microphone to automobile headlight reflectors to the design of ballistic missiles. They are frequently used in physics, engineering, and many other areas.
History
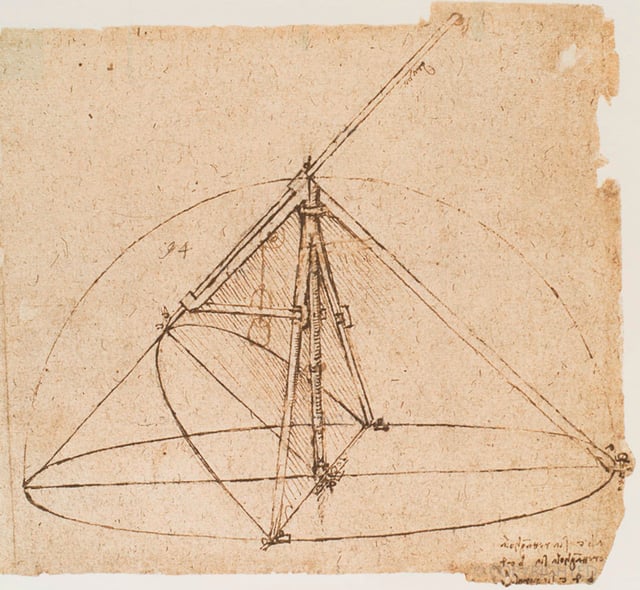
Parabolic compass designed by Leonardo da Vinci
The earliest known work on conic sections was by Menaechmus in the 4th century BC. He discovered a way to solve the problem of doubling the cube using parabolas. (The solution, however, does not meet the requirements of compass-and-straightedge construction.) The area enclosed by a parabola and a line segment, the so-called "parabola segment", was computed by Archimedes via the method of exhaustion in the 3rd century BC, in his The Quadrature of the Parabola. The name "parabola" is due to Apollonius who discovered many properties of conic sections. It means "application", referring to "application of areas" concept, that has a connection with this curve, as Apollonius had proved.[10] The focus–directrix property of the parabola and other conic sections is due to Pappus.
Galileo showed that the path of a projectile follows a parabola, a consequence of uniform acceleration due to gravity.
The idea that a parabolic reflector could produce an image was already well known before the invention of the reflecting telescope.[11] Designs were proposed in the early to mid seventeenth century by many mathematicians including René Descartes, Marin Mersenne,[12] and James Gregory.[13] When Isaac Newton built the first reflecting telescope in 1668, he skipped using a parabolic mirror because of the difficulty of fabrication, opting for a spherical mirror. Parabolic mirrors are used in most modern reflecting telescopes and in satellite dishes and radar receivers.[14]
Definition as a locus of points
A parabola can be defined geometrically as a set of points (locus of points) in the Euclidean plane:
A parabola is a set of points, such that for any point of the set the distance to a fixed point , the focus, is equal to the distance to a fixed line , the directrix:

 of the perpendicular from the focus
of the perpendicular from the focus onto the directrix
onto the directrix is called vertex and the line
is called vertex and the line the axis of symmetry of the parabola.
the axis of symmetry of the parabola.In a cartesian coordinate system
Axis of symmetry parallel to the y-axis

Parabola: Definition, p: semi-latus rectum

Parabola: axis parallel to y-axis

Parabola: general case
 and the directrix has the equation
and the directrix has the equation one obtains for a point
one obtains for a point from
from the equation
the equation . Solving for
. Solving for yields
yields .
.The parabola is U-shaped (opening to the top).
 . From the picture one obtains
. From the picture one obtains .
. is the radius of the osculating circle at the vertex. For a parabola, the semi-latus rectum,
is the radius of the osculating circle at the vertex. For a parabola, the semi-latus rectum, , is the distance of the focus from the directrix. Using the parameter
, is the distance of the focus from the directrix. Using the parameter , the equation of the parabola can be rewritten as
, the equation of the parabola can be rewritten as .
. , the focus
, the focus and the directrix
and the directrix , one obtains the equation
, one obtains the equation .
.Remark:
In the case of the parabola has a downwards opening.
The presumption that the axis is parallel to the y-axis allows one to consider a parabola as the graph of a polynomial of degree 2, and vice versa: the graph of an arbitrary polynomial of degree 2 is a parabola (see next section).
If one exchanges and , one obtains equations of the form . These parabolas open to the left (if ) or to the right (if ).
General case
 and the directrix
and the directrix one obtains the equation
one obtains the equation
 .)
.)For a parametric equation of a parabola in general position see § As the affine image of the unit parabola.
The implicit equation of a parabola is defined by an irreducible polynomial of degree two

 or, equivalently, such that
or, equivalently, such that is the square of alinear polynomial.
is the square of alinear polynomial.As a graph of a function

Parabolas
The previous section shows: any parabola with the origin as vertex and the y-axis as axis of symmetry can be considered as the graph of a function
 .
. the parabolas are opening to the top and for
the parabolas are opening to the top and for opening to the bottom (see picture). From the section above one obtains:
opening to the bottom (see picture). From the section above one obtains:The focus is ,
the focal length , the semi-latus rectum is ,
the vertex is ,
the directrix has the equation ,
the tangent at point has the equation ,
 the parabola is the unit parabola with equation
the parabola is the unit parabola with equation .
Its focus is
.
Its focus is , the semi-latus rectum
, the semi-latus rectum and the directrix has the equation
and the directrix has the equation .
.The general function of degree 2 is
 .
.Completing the square yields
 ,
,which is the equation of a parabola with
the axis (parallel to the y-axis),
the focal length , the semi-latus rectum ,
the vertex ,
the focus ,
the directrix ,
the point of the parabola intersecting the y-axis has coordinates ,
the tangent at a point on the y-axis has the equation .
Similarity to the unit parabola

When the parabola is uniformly scaled by factor 2, the result is the parabola
Two objects in the Euclidean plane are similar if one can be transformed to the other by a similarity, that is, an arbitrary composition of rigid motions (translations and rotations) and uniform scalings.
 with vertex
with vertex can be transformed by the translation
can be transformed by the translation to one with the origin as vertex. A suitable rotation around the origin can then transform the parabola to one that has they-axis as axis of symmetry. Hence the parabola
to one with the origin as vertex. A suitable rotation around the origin can then transform the parabola to one that has they-axis as axis of symmetry. Hence the parabola can be transformed by a rigid motion to a parabola with an equation
can be transformed by a rigid motion to a parabola with an equation . Such a parabola can then be transformed by theuniform scaling
. Such a parabola can then be transformed by theuniform scaling into the unit parabola with equation
into the unit parabola with equation . Thus, any parabola can be mapped to the unit parabola by a similarity.[15]
. Thus, any parabola can be mapped to the unit parabola by a similarity.[15]A synthetic approach, using similar triangles, can also be used to establish this result.[16]
The general result is that two conic sections (necessarily of the same type) are similar if and only if they have the same eccentricity.[15] Thus, only circles (all having eccentricity 0) share this property with parabolas (all having eccentricity 1), while general ellipses and hyperbolas do not.
 onto the unit parabola, such as
onto the unit parabola, such as . But this mapping is not a similarity, and only shows that all parabolas are affinely equivalent (see§ As the affine image of the unit parabola).
. But this mapping is not a similarity, and only shows that all parabolas are affinely equivalent (see§ As the affine image of the unit parabola).As a special conic section

Pencil of conics with a common vertex
 can be represented by the equation
can be represented by the equation ,
, theeccentricity.
theeccentricity.For the conic is a circle (osculating circle of the pencil),
for an ellipse,
for the parabola with equation and
for a hyperbola (see picture).
In polar coordinates

Pencil of conics with a common focus
 (opening to the right) has thepolar coordinaterepresentation:
(opening to the right) has thepolar coordinaterepresentation:![{\displaystyle r=2p{\frac {\cos \varphi }{\sin ^{2}\varphi }}{\text{ with }}\varphi \in \left[-{\tfrac {\pi }{2}},{\tfrac {\pi }{2}}\right]\setminus \{0\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41cad0aa45d52db95b00b62ac435525f4f867d04) (
( .)
.) and its focus is
and its focus is .
. , one obtains the equation
, one obtains the equation
Remark 1: Inverting this polar form shows: a parabola is the inverse of a cardioid.
 (see picture):
(see picture): , (
, ( : eccentricity).
: eccentricity).Conic section and quadratic form
Diagram, description, and definitions
The diagram represents a cone with its axis vertical.[2] The point A is its apex. An inclined cross-section of the cone, shown in pink, is inclined from the vertical by the same angle, θ, as the side of the cone. According to the definition of a parabola as a conic section, the boundary of this pink cross-section, EPD, is a parabola.
A horizontal cross-section of the cone passes through the vertex, P, of the parabola. This cross-section is circular, but appears elliptical when viewed obliquely, as is shown in the diagram. Its centre is V, and PK is a diameter. We will call its radius r.
Another horizontal, circular cross-section of the cone is farther from the apex, A, than the one just described. It has a chord DE, which joins the points where the parabola intersects the circle. Another chord, BC, is the perpendicular bisector of DE, and is consequently a diameter of the circle. These two chords and the parabola's axis of symmetry, PM, all intersect at the point M.
All the labelled points, except D and E, are coplanar. They are in the plane of symmetry of the whole figure. This includes the point F, which is not mentioned above. It is defined and discussed below, in the paragraph "Position of the focus".
Let us call the length of DM and of EM x, and the length of PM y.
Derivation of quadratic equation
The lengths of BM and CM are:
 (triangle BPM isisosceles.)
(triangle BPM isisosceles.) (PMCK is aparallelogram.)
(PMCK is aparallelogram.)Using the intersecting chords theorem on the chords BC and DE, we get:

Substituting:

Rearranging:

For any given cone and parabola, r and θ are constants, but x and y are variables which depend on the arbitrary height at which the horizontal cross-section BECD is made. This last equation shows the relationship between these variables. They can be interpreted as Cartesian coordinates of the points D and E, in a system in the pink plane with P as its origin. Since x is squared in the equation, the fact that D and E are on opposite sides of the y-axis is unimportant. If the horizontal cross-section moves up or down, toward or away from the apex of the cone, D and E move along the parabola, always maintaining the relationship between x and y shown in the equation. The parabolic curve is therefore the locus of points where the equation is satisfied, which makes it a Cartesian graph of the quadratic function in the equation.
This discussion started from the definition of a parabola as a conic section, but it has now led to a description as a graph of a quadratic function. This shows that these two descriptions are equivalent. They both define curves of exactly the same shape.
Focal length
It is proved in a preceding section that if a parabola has its vertex at the origin, and if it opens in the positive y direction, then its equation is y = x2/4f, where f is its focal length.[3] Comparing this with the last equation above shows that the focal length of the parabola in the cone is r sin θ.
Position of the focus
In the diagram above, the point V is the foot of the perpendicular from the vertex of the parabola to the axis of the cone. The point F is the foot of the perpendicular from the point V to the plane of the parabola.[4] By symmetry, F is on the axis of symmetry of the parabola. Angle VPF is complementary to θ, and angle PVF is complementary to angle VPF, therefore angle PVF is θ. Since the length of PV is r, the distance of F from the vertex of the parabola is r sin θ. It is shown above that this distance equals the focal length of the parabola, which is the distance from the vertex to the focus. The focus and the point F are therefore equally distant from the vertex, along the same line, which implies that they are the same point. Therefore, the point F, defined above, is the focus of the parabola.
Alternative proof with Dandelin spheres
An alternative proof can be done using Dandelin spheres. It works without calculation and uses elementary geometric considerations, only. (see German article on Parabel)
Proof of the reflective property

Reflective property of a parabola
The reflective property states that, if a parabola can reflect light, then light which enters it travelling parallel to the axis of symmetry is reflected toward the focus. This is derived from the wave nature of light in the paragraph "description of final diagram", which describes a diagram just above it, at the end of this article. This derivation is valid, but may not be satisfying to readers who would prefer a mathematical approach. In the following proof, the fact that every point on the parabola is equidistant from the focus and from the directrix is taken as axiomatic.
Consider the parabola y = x2. Since all parabolas are similar, this simple case represents all others. The right-hand side of the diagram shows part of this parabola.
Construction and definitions
The point E is an arbitrary point on the parabola, with coordinates (x, x2). The focus is F, the vertex is A (the origin), and the line FA (the y-axis) is the axis of symmetry. The line EC is parallel to the axis of symmetry, and intersects the x-axis at D. The point C is located on the directrix (which is not shown, to minimize clutter). The point B is the midpoint of the line segment FC.
Deductions
Measured along the axis of symmetry, the vertex, A, is equidistant from the focus, F, and from the directrix. According to the Intercept theorem, since C is on the directrix, the y-coordinates of F and C are equal in absolute value and opposite in sign. B is the midpoint of FC, so its y-coordinate is zero, so it lies on the x-axis. Its x-coordinate is half that of E, D, and C, i.e., x/2. The slope of the line BE is the quotient of the lengths of ED and BD, which is x2/x/2, which comes to 2x. But 2x is also the slope (first derivative) of the parabola at E. Therefore, the line BE is the tangent to the parabola at E.
The distances EF and EC are equal because E is on the parabola, F is the focus and C is on the directrix. Therefore, since B is the midpoint of FC, triangles △FEB and △CEB are congruent (three sides), which implies that the angles marked α are congruent. (The angle above E is vertically opposite angle ∠BEC.) This means that a ray of light which enters the parabola and arrives at E travelling parallel to the axis of symmetry will be reflected by the line BE so it travels along the line EF, as shown in red in the diagram (assuming that the lines can somehow reflect light). Since BE is the tangent to the parabola at E, the same reflection will be done by an infinitesimal arc of the parabola at E. Therefore, light that enters the parabola and arrives at E travelling parallel to the axis of symmetry of the parabola is reflected by the parabola toward its focus.
The point E has no special characteristics. This conclusion about reflected light applies to all points on the parabola, as is shown on the left side of the diagram. This is the reflective property.
Other consequences
There are other theorems that can be deduced simply from the above argument.
Tangent bisection property
The above proof and the accompanying diagram show that the tangent BE bisects the angle ∠FEC. In other words, the tangent to the parabola at any point bisects the angle between the lines joining the point to the focus, and perpendicularly to the directrix.
Intersection of a tangent and perpendicular from focus

Perpendicular from focus to tangent
Since triangles △FBE and △CBE are congruent, FB is perpendicular to the tangent BE. Since B is on the x-axis, which is the tangent to the parabola at its vertex, it follows that the point of intersection between any tangent to a parabola and the perpendicular from the focus to that tangent lies on the line that is tangential to the parabola at its vertex. See animated diagram [17] and pedal curve.
Reflection of light striking the convex side
If light travels along the line CE, it moves parallel to the axis of symmetry and strikes the convex side of the parabola at E. It is clear from the above diagram that this light will be reflected directly away from the focus, along an extension of the segment FE.
Alternative proofs

Parabola and tangent
The above proofs of the reflective and tangent bisection properties use a line of calculus. For readers who are not comfortable with calculus, the following alternative is presented.
In this diagram, F is the focus of the parabola, and T and U lie on its directrix. P is an arbitrary point on the parabola. PT is perpendicular to the directrix, and the line MP bisects angle ∠FPT. Q is another point on the parabola, with QU perpendicular to the directrix. We know that FP = PT and FQ = QU. Clearly, QT > QU, so QT > FQ. All points on the bisector MP are equidistant from F and T, but Q is closer to F than to T. This means that Q is to the left of MP, i.e., on the same side of it as the focus. The same would be true if Q were located anywhere else on the parabola (except at the point P), so the entire parabola, except the point P, is on the focus side of MP. Therefore, MP is the tangent to the parabola at P. Since it bisects the angle ∠FPT, this proves the tangent bisection property.
The logic of the last paragraph can be applied to modify the above proof of the reflective property. It effectively proves the line BE to be the tangent to the parabola at E if the angles α are equal. The reflective property follows as shown previously.
Pin and string construction

Parabola: pin string construction
The definition of a parabola by its focus and directrix can be used for drawing it with help of pins and strings [18]:
 and the directrix
and the directrix of the parabola.(1) Take a triangle of a set square and prepare a string with length
of the parabola.(1) Take a triangle of a set square and prepare a string with length (see diagram).(2) Pin one end of the string at point
(see diagram).(2) Pin one end of the string at point of the triangle and the other one to the focus
of the triangle and the other one to the focus .(3) Position the triangle such that the second edge of the right angle is free to slide along the directrix.(4) Take a pen and hold the string tight to the triangle.(5) While moving the triangle along the directrix the pen draws an arc of a parabola, because of
.(3) Position the triangle such that the second edge of the right angle is free to slide along the directrix.(4) Take a pen and hold the string tight to the triangle.(5) While moving the triangle along the directrix the pen draws an arc of a parabola, because of (see definition of a parabola).
(see definition of a parabola).Properties related to Pascal's theorem
 on the line of infinity
on the line of infinity , which is the tangent at
, which is the tangent at . The 5-,4- and 3- point degenerations ofPascal's theoremare properties of a conic dealing with at least one tangent. If one considers this tangent as the line at infinity and its point of contact as the point at infinity of the y-axis, one obtains three statements for a parabola.
. The 5-,4- and 3- point degenerations ofPascal's theoremare properties of a conic dealing with at least one tangent. If one considers this tangent as the line at infinity and its point of contact as the point at infinity of the y-axis, one obtains three statements for a parabola. .
.4-points-property

4-points-property of a parabola
 .
.Let be four points of the parabola and the intersection of the secant line with the line and let be the intersection of the secant line with the line (see picture). Then the secant line is parallel to line .
- (The lines
 and
and are parallel to the axis of the parabola.)
are parallel to the axis of the parabola.) .
. , while
, while and
and are given.
are given.Remark: the 4-points-property of a parabola is an affine version of the 5-point-degeneration of Pascal's theorem.
3-points-1-tangent-property

3-points-1-tangent-property
Let be three points of the parabola with equation and the intersection of the secant line with the line and the intersection of the secant line with the line (see picture), then the tangent at point is parallel to the line .
- (The lines
 and
and are parallel to the axis of the parabola.)
are parallel to the axis of the parabola.) . A short calculation shows: line
. A short calculation shows: line has slope
has slope which is the slope of the tangent at point
which is the slope of the tangent at point .
. , while
, while are given.
are given.Remark: The 3-points-1-tangent-property of a parabola is an affine version of the 4-point-degeneration of Pascal's theorem.
2-points-2-tangents-property

2-points-2-tangents-property
Let be two points of the parabola with equation and the intersection of the tangent at point with the line and the intersection of the tangent at point with the line (see picture) then the secant is parallel to the line .
- (The lines
 and
and are parallel to the axis of the parabola.)
are parallel to the axis of the parabola.) .
. while
while and the tangent at
and the tangent at are given.
are given.Remark 1: The 2-points-2-tangents-property of a parabola is an affine version of the 3-point-degeneration of Pascal's theorem.
Remark 2: The 2-points-2-tangents-property should not be confused with the following property of a parabola, which deals with 2 points and 2 tangents, too, but is not related to Pascal's theorem.
Axis-direction

Construction of the axis-direction
 . The following property determines the points
. The following property determines the points by two given points and their tangents only, and the result is: the line
by two given points and their tangents only, and the result is: the line is parallel to the axis of the parabola.
is parallel to the axis of the parabola.Let be two points of the parabola and be their tangents; be the intersection of the tangents , be the intersection of the parallel line to through with the parallel line to through (see picture). Then the line is parallel to the axis of the parabola and has the equation
 .
.Application: This property can be used to determine the direction of the axis of a parabola, if two points and their tangents are given. An alternative way is to determine the midpoints of two parallel chords, see section on parallel chords.
Remark: This property is an affine version of the theorem of two perspective triangles of a non-degenerate conic.[19]
Steiner generation
Parabola

Steiner generation of a parabola
Steiner established the following procedure for the construction of a non-degenerate conic (see Steiner conic):
Given two pencils of lines at two points (all lines containing and respectively) and a projective but not perspective mapping of onto . Then the intersection points of corresponding lines form a non-degenerate projective conic section.
 :
:Consider the pencil at the vertex and the set of lines , which are parallel to the y-axis.
Let be a point on the parabola and , .
The line segment is divided into n equally spaced segments and this division is projected (in the direction ) onto the line segment (see figure). This projection gives rise to a projective mapping from pencil onto the pencil .
The intersection of the line and the i-th parallel to the y-axis is a point on the parabola.
Proof: straightforward calculation.
Remark: Steiner's generation is also available for ellipses and hyperbolas.
Dual parabola

Dual parabola and Bezier curve of degree 2 (right: curve point and division points for parameter )
A dual parabola consists of the set of tangents of an ordinary parabola.
The Steiner generation of a conic can be applied to the generation of a dual conic by changing the meanings of points and lines:
Let be given two point sets on two lines and a projective but not perspective mapping between these point sets, then the connecting lines of corresponding points form a non degenerate dual conic.
In order to generate elements of a dual parabola, one starts with
three points not on a line,
divides the line sections and each into equally spaced line segments and adds numbers as shown in the picture.
Then the lines are tangents of a parabola, hence elements of a dual parabola.
The parabola is a Bezier curve of degree 2 with the control points .
The proof is a consequence of the de Casteljau algorithm for a Bezier curve of degree 2.
Inscribed angles and the 3-point-form

Inscribed angles of a parabola
 is uniquely determined by three points
is uniquely determined by three points with different x-coordinates. The usual procedure to determine the coefficients
with different x-coordinates. The usual procedure to determine the coefficients is to insert the point coordinates into the equation. The result is a linear system of three equations, which can be solved byGaussian eliminationorCramer's rule, for example. An alternative way uses the inscribed angle theorem for parabolas:
is to insert the point coordinates into the equation. The result is a linear system of three equations, which can be solved byGaussian eliminationorCramer's rule, for example. An alternative way uses the inscribed angle theorem for parabolas: the angle between two lines of equations
the angle between two lines of equations is measured by
is measured by
- Four points
 with differentx-coordinates (see picture), are on a parabola with equation
with differentx-coordinates (see picture), are on a parabola with equation if and only if the angles at
if and only if the angles at and
and have the same measure, as defined above. That is,
have the same measure, as defined above. That is,
 then one has
then one has if the points are on the parabola.)
if the points are on the parabola.) ) of the parabola determined by 3 points
) of the parabola determined by 3 points with differentx-coordinates is (if twox-coordinates are equal there is no parabola with directrix parallel to thex-axis, which passes through the points)
with differentx-coordinates is (if twox-coordinates are equal there is no parabola with directrix parallel to thex-axis, which passes through the points)
 one obtains the more standard form
one obtains the more standard form
Pole-polar relation

Parabola: pol-polar-relation
 . The equation of the tangent at a point
. The equation of the tangent at a point is
is .
.One obtains the function

on the set of points of the parabola onto the set of tangents.
 to a bijection between the points of
to a bijection between the points of and the lines with equations
and the lines with equations . The inverse mapping is
. The inverse mapping is- line
 point
point .
.This relation is called the pole-polar relation of the parabola, where the point is the pole and the corresponding line its polar.
By calculation one checks the following properties of the pole-polar relation of the parabola:
For a point (pole) on the parabola the polar is the tangent at this point (see picture: ).
For a pole outside the parabola the intersection points of its polar with the parabola are the touching points of the two tangents passing (see picture: ).
For a point within the parabola the polar has no point with the parabola in common. (see picture: and ).
The intersection point of two polar lines (for example: ) is the pole of the connecting line of their poles (in example: ).
focus and directrix of the parabola are a pole-polar pair.
Remark: Pole-polar relations exist for ellipses and hyperbolas, too.
Tangent properties
Two tangent properties related to the latus rectum

Perpendicular tangents intersect on the directrix
Let the line of symmetry intersect the parabola at point Q, and denote the focus as point F and its distance from point Q as f. Let the perpendicular to the line of symmetry, through the focus, intersect the parabola at a point T. Then (1) the distance from F to T is 2f, and (2) a tangent to the parabola at point T intersects the line of symmetry at a 45° angle.[22] []
If two tangents to a parabola are perpendicular to each other, then they intersect on the directrix. Conversely, two tangents which intersect on the directrix are perpendicular.
Lambert's theorem
Tsukerman's converse to Lambert's theorem states that, given three lines that bound a triangle, if two of the lines are tangent to a parabola whose focus lies on the circumcircle of the triangle, then the third line is also tangent to the parabola.[24]
Facts related to chords
Focal length calculated from parameters of a chord
Suppose a chord crosses a parabola perpendicular to its axis of symmetry. Let the length of the chord between the points where it intersects the parabola be c and the distance from the vertex of the parabola to the chord, measured along the axis of symmetry, be d. The focal length, f, of the parabola is given by:

- Proof
Suppose a system of Cartesian coordinates is used such that the vertex of the parabola is at the origin, and the axis of symmetry is the y-axis. The parabola opens upward. It is shown elsewhere in this article that the equation of the parabola is 4fy = x2, where f is the focal length. At the positive x end of the chord, x = c/2 and y = d. Since this point is on the parabola, these coordinates must satisfy the equation above. Therefore, by substitution, 4fd = (c/2)2. From this, f = c2/16d.
Area enclosed between a parabola and a chord
Arc length
If a point X is located on a parabola which has focal length f, and if p is the perpendicular distance from X to the axis of symmetry of the parabola, then the lengths of arcs of the parabola which terminate at X can be calculated from f and p as follows, assuming they are all expressed in the same units.[8]

This quantity, s, is the length of the arc between X and the vertex of the parabola.
The length of the arc between X and the symmetrically opposite point on the other side of the parabola is 2s.
The perpendicular distance, p, can be given a positive or negative sign to indicate on which side of the axis of symmetry X is situated. Reversing the sign of p reverses the signs of h and s without changing their absolute values. If these quantities are signed, any The calculation can be simplified by using the properties of logarithms:

This can be useful, for example, in calculating the size of the material needed to make a parabolic reflector or parabolic trough.
This calculation can be used for a parabola in any orientation. It is not restricted to the situation where the axis of symmetry is parallel to the y-axis.
A geometrical construction to find a sector area
[[INLINE_IMAGE|//upload.wikimedia.org/wikipedia/commons/f/f3/Sector_Area_Prop_30.png|undefined|Sector Area Prop 30|h395|w510]]
S is the Focus and V is the Principal Vertex of the parabola VG. Draw VX perpendicular to SV.
Take any point B on VG and drop a perpendicular BQ from B to VX. Draw perpendicular ST intersecting BQ, extended if necessary, at T. At B draw the perpendicular BJ, intersecting VX at J.


Since triangles TSB and QBJ are similar:

 , and can be found from the length of VJ, as found above.
, and can be found from the length of VJ, as found above.A circle through S, V and B also passes through J.
Conversely, if a point, B on the parabola VG is to be found so that the Area of the Sector SVB is equal to a specified value, determine the point J on VX, and construct a circle through S, V and J. Since SJ is the diameter, the center of the circle is at its midpoint, and it lies on the perpendicular bisector of SV, a distance of one half VJ from SV. The point required, B is where this circle intersects the parabola.
If a body traces the path of the parabola due to an inverse square force directed towards S, the area SVB increases at a constant rate as point B moves forward. It follows that J moves at constant speed along VX as B moves along the parabola.
If the speed of the body at the vertex, where it is moving perpendicularly to SV is v, then the speed of J is equal to 3v/4.

 , and point J moves at a constant speed of
, and point J moves at a constant speed of
The above construction was devised by Isaac Newton and can be found in Book 1 of the Principia as Proposition 30.
Focal length and radius of curvature at the vertex
The focal length of a parabola is half of its radius of curvature at its vertex.
- Proof
Consider a point (x, y) on a circle of radius R and with center at the point (0, R). The circle passes through the origin. If the point is near the origin, the Pythagorean theorem shows that:

But if (x, y) is extremely close to the origin, since the x-axis is a tangent to the circle, y is very small compared with x, so y2 is negligible compared with the other terms. Therefore, extremely close to the origin:
 (Equation 1)
(Equation 1)Compare this with the parabola:
 (Equation 2)
(Equation 2)which has its vertex at the origin, opens upward, and has focal length f. (See preceding sections of this article.)
Equations 1 and 2 are equivalent if R = 2f. Therefore, this is the condition for the circle and parabola to coincide at and extremely close to the origin. The radius of curvature at the origin, which is the vertex of the parabola, is twice the focal length.
- Corollary
A concave mirror which is a small segment of a sphere behaves approximately like a parabolic mirror, focusing parallel light to a point which is midway between the centre and the surface of the sphere.
As the affine image of the unit parabola

Parabola as an affine image of the unit parabola
Another definition of a parabola uses affine transformations:
Any parabola is the affine image of the unit parabola with equation .
 , where
, where is a regular matrix (determinant is not 0) and
is a regular matrix (determinant is not 0) and is an arbitrary vector. If
is an arbitrary vector. If are the column vectors of the matrix
are the column vectors of the matrix , the unit parabola
, the unit parabola is mapped onto the parabola
is mapped onto the parabola is a point of the parabola and
is a point of the parabola and is a tangent vector at point
is a tangent vector at point .
. is parallel to the axis of the parabola (axis of symmetry through the vertex).
is parallel to the axis of the parabola (axis of symmetry through the vertex). are not perpendicular and
are not perpendicular and is not the vertex, unless the affine transformation is asimilarity.
is not the vertex, unless the affine transformation is asimilarity. is
is . At the vertex the tangent vector is orthogonal to
. At the vertex the tangent vector is orthogonal to . Hence the parameter
. Hence the parameter of the vertex is the solution of the equation
of the vertex is the solution of the equation , which is
, which is and
and is the vertex.
is the vertex.The focal length can be determined by a suitable parameter transformation (which does not change the geometric shape of the parabola). The focal length is
 .
.Hence
 is the focus of the parabola.
is the focus of the parabola. are vectors of the Euclidean space.
are vectors of the Euclidean space.As quadratic Bézier curve
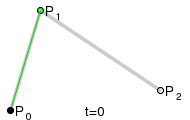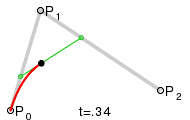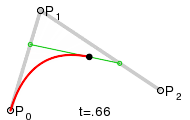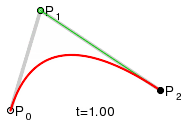
Quadratic Bézier curve and its control points

Simpson's rule: the graph of a function is replaced by an arc of a parabola
 defined by three points
defined by three points ,
, and
and , its control points:
, its control points:![{\displaystyle {\begin{aligned}{\vec {c}}(t)\ &=\ \sum _{i=0}^{2}{\binom {2}{i}}t^{i}(1-t)^{2-i}{\vec {p}}_{i}\\\ &=\ (1-t)^{2}{\vec {p}}_{0}+2t(1-t){\vec {p}}_{1}+t^{2}{\vec {p}}_{2}\\\ &=\ ({\vec {p}}_{0}-2{\vec {p}}_{1}+{\vec {p}}_{2})t^{2}+(-2{\vec {p}}_{0}+2{\vec {p}}_{1})t+{\vec {p}}_{0}{\text{ , }}t\in [0,1]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0156d961ce6bdb1e3296ec962a61d8b567b24547)
This curve is an arc of a parabola (see § As the affine image of the unit parabola).
Numerical integration
In one method of numerical integration one replaces the graph of a function by arcs of parabolas and integrates the parabola arcs. A parabola is determined by three points. The formula for one arc is

The method is called Simpson's rule.
As plane section of quadric
The following quadrics contain parabolas as plane sections:
Elliptical Cone
Parabolic cylinder
Elliptical paraboloid
Hyperbolic paraboloid
Hyperboloid of one sheet
Hyperboloid of two sheets
As trisectrix

Angle trisection with a parabola
A parabola can be used as a trisectrix, that is it allows the exact trisection of an arbitrary angle with straightedge and compass. This is not in contradiction to the impossibility of an angle trisection with compass-and-straightedge constructions alone, as the use of parabolas is not allowed in the classic rules for compass-and-straightedge constructions.
 place its leg
place its leg on the x-axis such that the vertex
on the x-axis such that the vertex is in the coordinate system's origin. The coordinate system also contains the parabola
is in the coordinate system's origin. The coordinate system also contains the parabola . The unit circle with radius 1 around the origin intersects the angle's other leg
. The unit circle with radius 1 around the origin intersects the angle's other leg and from this point of intersection draw the perpendicular onto the y-axis. The parallel to y-axis through the midpoint of that perpendicular and the tangent on the unit circle in
and from this point of intersection draw the perpendicular onto the y-axis. The parallel to y-axis through the midpoint of that perpendicular and the tangent on the unit circle in intersect in
intersect in . The circle around
. The circle around with radius
with radius intersects the parabola in
intersects the parabola in . The perpendicular from
. The perpendicular from onto the x-axis intersects the unit circle in
onto the x-axis intersects the unit circle in and
and is exactly one third of
is exactly one third of .
. is
is . Solving the equation system given by the circle around
. Solving the equation system given by the circle around and the parabola leads to the cubic equation
and the parabola leads to the cubic equation . Thetriple angle formula
. Thetriple angle formula then shows that
then shows that is indeed a solution of that cubic equation.
is indeed a solution of that cubic equation.This trisection goes back to René Descartes who described it in his book La Geometria (1637).[27]
Generalizations
 are still valid: 1) a line intersects in at most two points. 2) At any point
are still valid: 1) a line intersects in at most two points. 2) At any point the line
the line is the tangent.... Essentially new phenomena arise, if the field has characteristic 2 (i.e.,
is the tangent.... Essentially new phenomena arise, if the field has characteristic 2 (i.e., ) : the tangents are all parallel.
) : the tangents are all parallel.In algebraic geometry, the parabola is generalized by the rational normal curves, which have coordinates (x, x2, x3,…,xn); the standard parabola is the case n =2, and the case n = 3 is known as the twisted cubic. A further generalization is given by the Veronese variety, when there is more than one input variable.
In the theory of quadratic forms, the parabola is the graph of the quadratic form x2 (or other scalings), while the elliptic paraboloid is the graph of the positive-definite quadratic form x2 + y2 (or scalings) and the hyperbolic paraboloid is the graph of the indefinite quadratic form x2 − y2. Generalizations to more variables yield further such objects.
The curves y = x**p for other values of p are traditionally referred to as the higher parabolas, and were originally treated implicitly, in the form x**p = ky**q for p and q both positive integers, in which form they are seen to be algebraic curves. These correspond to the explicit formula y = x**p/q for a positive fractional power of x. Negative fractional powers correspond to the implicit equation xpy**q = k, and are traditionally referred to as higher hyperbolas. Analytically, x can also be raised to an irrational power (for positive values of x); the analytic properties are analogous to when x is raised to rational powers, but the resulting curve is no longer algebraic, and cannot be analyzed via algebraic geometry.
In the physical world
In nature, approximations of parabolas and paraboloids are found in many diverse situations. The best-known instance of the parabola in the history of physics is the trajectory of a particle or body in motion under the influence of a uniform gravitational field without air resistance (for instance, a ball flying through the air, neglecting air friction).
The parabolic trajectory of projectiles was discovered experimentally in the early 17th century by Galileo, who performed experiments with balls rolling on inclined planes. He also later proved this mathematically in his book Dialogue Concerning Two New Sciences.[28][9] For objects extended in space, such as a diver jumping from a diving board, the object itself follows a complex motion as it rotates, but the center of mass of the object nevertheless forms a parabola. As in all cases in the physical world, the trajectory is always an approximation of a parabola. The presence of air resistance, for example, always distorts the shape, although at low speeds, the shape is a good approximation of a parabola. At higher speeds, such as in ballistics, the shape is highly distorted and doesn't resemble a parabola.
Another hypothetical situation in which parabolas might arise, according to the theories of physics described in the 17th and 18th centuries by Sir Isaac Newton, is in two-body orbits; for example the path of a small planetoid or other object under the influence of the gravitation of the Sun. Parabolic orbits do not occur in nature; simple orbits most commonly resemble hyperbolas or ellipses. The parabolic orbit is the degenerate intermediate case between those two types of ideal orbit. An object following a parabolic orbit would travel at the exact escape velocity of the object it orbits; objects in elliptical or hyperbolic orbits travel at less or greater than escape velocity, respectively. Long-period comets travel close to the Sun's escape velocity while they are moving through the inner solar system, so their paths are near parabolic.
Approximations of parabolas are also found in the shape of the main cables on a simple suspension bridge. The curve of the chains of a suspension bridge is always an intermediate curve between a parabola and a catenary, but in practice the curve is generally nearer to a parabola, and in calculations the second degree parabola is used.[29][30] Under the influence of a uniform load (such as a horizontal suspended deck), the otherwise catenary-shaped cable is deformed toward a parabola. Unlike an inelastic chain, a freely hanging spring of zero unstressed length takes the shape of a parabola. Suspension-bridge cables are, ideally, purely in tension, without having to carry other, e.g., bending, forces. Similarly, the structures of parabolic arches are purely in compression.
Paraboloids arise in several physical situations as well. The best-known instance is the parabolic reflector, which is a mirror or similar reflective device that concentrates light or other forms of electromagnetic radiation to a common focal point, or conversely, collimates light from a point source at the focus into a parallel beam. The principle of the parabolic reflector may have been discovered in the 3rd century BC by the geometer Archimedes, who, according to a dubious legend,[31] constructed parabolic mirrors to defend Syracuse against the Roman fleet, by concentrating the sun's rays to set fire to the decks of the Roman ships. The principle was applied to telescopes in the 17th century. Today, paraboloid reflectors can be commonly observed throughout much of the world in microwave and satellite-dish receiving and transmitting antennas.
In parabolic microphones, a parabolic reflector is used to focus sound onto a microphone, giving it highly directional performance.
Paraboloids are also observed in the surface of a liquid confined to a container and rotated around the central axis. In this case, the centrifugal force causes the liquid to climb the walls of the container, forming a parabolic surface. This is the principle behind the liquid mirror telescope.
Aircraft used to create a weightless state for purposes of experimentation, such as NASA's "Vomit Comet", follow a vertically parabolic trajectory for brief periods in order to trace the course of an object in free fall, which produces the same effect as zero gravity for most purposes.
In the United States, vertical curves in roads are usually parabolic by design.
Gallery
Click on any image to enlarge it.