Moment of inertia
Moment of inertia
| Moment of inertia | |
|---|---|
Common symbols | I |
| SI unit | kg m2 |
Other units | lbf·ft·s2 |
| Extensive? | yes |
Derivations from other quantities | |
| Dimension | M L2 |
Tightrope walkers use the moment of inertia of a long rod for balance as they walk the rope. Samuel Dixon crossing the Niagara River in 1890.
The moment of inertia, otherwise known as the angular mass or rotational inertia, of a rigid body is a quantity that determines the torque needed for a desired angular acceleration about a rotational axis; similar to how mass determines the force needed for a desired acceleration. It depends on the body's mass distribution and the axis chosen, with larger moments requiring more torque to change the body's rotation rate. It is an extensive (additive) property: for a point mass the moment of inertia is just the mass times the square of the perpendicular distance to the rotation axis. The moment of inertia of a rigid composite system is the sum of the moments of inertia of its component subsystems (all taken about the same axis). Its simplest definition is the second moment of mass with respect to distance from an axis. For bodies constrained to rotate in a plane, only their moment of inertia about an axis perpendicular to the plane, a scalar value, matters. For bodies free to rotate in three dimensions, their moments can be described by a symmetric 3 × 3 matrix, with a set of mutually perpendicular principal axes for which this matrix is diagonal and torques around the axes act independently of each other.
| Moment of inertia | |
|---|---|
Common symbols | I |
| SI unit | kg m2 |
Other units | lbf·ft·s2 |
| Extensive? | yes |
Derivations from other quantities | |
| Dimension | M L2 |
Introduction
When a body is free to rotate around an axis, torque must be applied to change its angular momentum. The amount of torque needed to cause any given angular acceleration (the rate of change in angular velocity) is proportional to the moment of inertia of the body. Moment of inertia may be expressed in units of kilogram meter squared (kg·m2) in SI units and pound-foot-second squared (lbf·ft·s2) in imperial or US units.
In 1673 Christiaan Huygens introduced this parameter in his study of the oscillation of a body hanging from a pivot, known as a compound pendulum.[1] The term moment of inertia was introduced by Leonhard Euler in his book Theoria motus corporum solidorum seu rigidorum in 1765,[1][2] and it is incorporated into Euler's second law.
The natural frequency of oscillation of a compound pendulum is obtained from the ratio of the torque imposed by gravity on the mass of the pendulum to the resistance to acceleration defined by the moment of inertia. Comparison of this natural frequency to that of a simple pendulum consisting of a single point of mass provides a mathematical formulation for moment of inertia of an extended body.[3][4]
Moment of inertia also appears in momentum, kinetic energy, and in Newton's laws of motion for a rigid body as a physical parameter that combines its shape and mass. There is an interesting difference in the way moment of inertia appears in planar and spatial movement. Planar movement has a single scalar that defines the moment of inertia, while for spatial movement the same calculations yield a 3 × 3 matrix of moments of inertia, called the inertia matrix or inertia tensor.[5][6]
The moment of inertia of a rotating flywheel is used in a machine to resist variations in applied torque to smooth its rotational output. The moment of inertia of an airplane about its longitudinal, horizontal and vertical axis determines how steering forces on the control surfaces of its wings, elevators and tail affect the plane in roll, pitch and yaw.
Definition
Spinning figure skaters can reduce their moment of inertia by pulling in their arms, allowing them to spin faster due to conservation of angular momentum.
Video of rotating chair experiment, illustrating moment of inertia. When the spinning professor pulls his arms, his moment of inertia decreases; to conserve angular momentum, his angular velocity increases.
If the angular momentum of a system is constant, then as the moment of inertia gets smaller, the angular velocity must increase. This occurs when spinning figure skaters pull in their outstretched arms or divers curl their bodies into a tuck position during a dive, to spin faster.[7][8][9][10][11][12][13]
Examples
Simple pendulum
using a similar derivation to the previous equation.
Similarly, the kinetic energy of the pendulum mass is defined by the velocity of the pendulum around the pivot to yield
Compound pendulum
Pendulums used in Mendenhall gravimeter apparatus, from 1897 scientific journal. The portable gravimeter developed in 1890 by Thomas C. Mendenhall provided the most accurate relative measurements of the local gravitational field of the Earth.
Center of oscillation
or
Notice that the distance to the center of oscillation of the seconds pendulum must be adjusted to accommodate different values for the local acceleration of gravity. Kater's pendulum is a compound pendulum that uses this property to measure the local acceleration of gravity, and is called a gravimeter.
Measuring moment of inertia
The moment of inertia of a complex system such as a vehicle or airplane around its vertical axis can be measured by suspending the system from three points to form a trifilar pendulum. A trifilar pendulum is a platform supported by three wires designed to oscillate in torsion around its vertical centroidal axis.[19] The period of oscillation of the trifilar pendulum yields the moment of inertia of the system.[20]
Motion in a fixed plane
Point mass
Four objects with identical masses and radii racing down a plane while rolling without slipping. From back to front: spherical shell, solid sphere, cylindrical ring, and solid cylinder. The time for each object to reach the finishing line depends on their moment of inertia. (OGV version)
Thus, moment of inertia is a physical property that combines the mass and distribution of the particles around the rotation axis. Notice that rotation about different axes of the same body yield different moments of inertia.
The moment of inertia of a continuous body rotating about a specified axis is calculated in the same way, except with infinitely many point particles. Thus the limits of summation are removed, and the sum is written as follows:
Another expression replaces the summation with an integral,
- and
Examples
The moment of inertia of a compound pendulum constructed from a thin disc mounted at the end of a thin rod that oscillates around a pivot at the other end of the rod, begins with the calculation of the moment of inertia of the thin rod and thin disc about their respective centers of mass.[18]
A list of moments of inertia formulas for standard body shapes provides a way to obtain the moment of inertia of a complex body as an assembly of simpler shaped bodies. The parallel axis theorem is used to shift the reference point of the individual bodies to the reference point of the assembly.
Rigid body
This defines the relative position vector and the velocity vector for the rigid system of the particles moving in a plane.
Note on the cross product: When a body moves parallel to a ground plane, the trajectories of all the points in the body lie in planes parallel to this ground plane. This means that any rotation that the body undergoes must be around an axis perpendicular to this plane. Planar movement is often presented as projected onto this ground plane so that the axis of rotation appears as a point. In this case, the angular velocity and angular acceleration of the body are scalars and the fact that they are vectors along the rotation axis is ignored. This is usually preferred for introductions to the topic. But in the case of moment of inertia, the combination of mass and geometry benefits from the geometric properties of the cross product. For this reason, in this section on planar movement the angular velocity and accelerations of the body are vectors perpendicular to the ground plane, and the cross product operations are the same as used for the study of spatial rigid body movement.
Angular momentum
For a given amount of angular momentum, a decrease in the moment of inertia results in an increase in the angular velocity. Figure skaters can change their moment of inertia by pulling in their arms. Thus, the angular velocity achieved by a skater with outstretched arms results in a greater angular velocity when the arms are pulled in, because of the reduced moment of inertia. A figure skater is not, however, a rigid body.
Kinetic energy
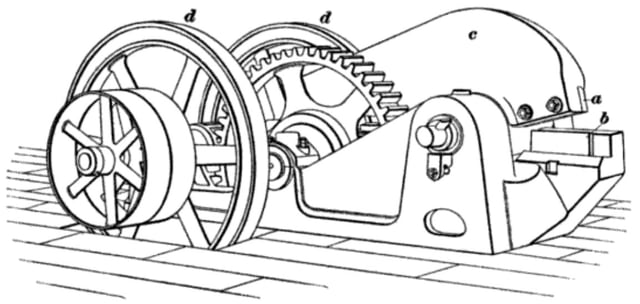
This 1906 rotary shear uses the moment of inertia of two flywheels to store kinetic energy which when released is used to cut metal stock (International Library of Technology, 1906).
Newton's laws
A 1920s John Deere tractor with the spoked flywheel on the engine. The large moment of inertia of the flywheel smooths the operation of the tractor
This yields the resultant torque on the system as
Motion in space of a rigid body, and the inertia matrix
The scalar moments of inertia appear as elements in a matrix when a system of particles is assembled into a rigid body that moves in three-dimensional space. This inertia matrix appears in the calculation of the angular momentum, kinetic energy and resultant torque of the rigid system of particles.[3][4][5][6][25]
and the (absolute) velocities are
Angular momentum
![{\displaystyle \left[\mathbf {b} \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ce9643510bd433e0ed612edd5d3a9ed7faecfec)
![{\displaystyle {\begin{aligned}\mathbf {b} \times \mathbf {y} &\equiv \left[\mathbf {b} \right]\mathbf {y} \\\left[\mathbf {b} \right]&\equiv {\begin{bmatrix}0&-b_{z}&b_{y}\\b_{z}&0&-b_{x}\\-b_{y}&b_{x}&0\end{bmatrix}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4782eb664e98a6d680dd96b77601ff9bc12ab4a)
![{\displaystyle [\Delta \mathbf {r} _{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ee5960e77611f673ab2f2050f356dbf0e403132)
![{\displaystyle \mathbf {L} =\left(-\sum _{i=1}^{n}m_{i}\left[\Delta \mathbf {r} _{i}\right]^{2}\right){\boldsymbol {\omega }}=\mathbf {I} _{\mathbf {C} }{\boldsymbol {\omega }},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26ff4f4ab9aa3fff11085b8828fc71a4af7de700)
![{\displaystyle \mathbf {I} _{\mathbf {C} }=-\sum _{i=1}^{n}m_{i}\left[\Delta \mathbf {r} _{i}\right]^{2},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6766e8a9ce07ff8f32ec86aaa929f1e5a3ce1a21)
Kinetic energy
This equation expands to yield three terms
![{\displaystyle {\begin{aligned}E_{\text{K}}&={\frac {1}{2}}\left(\sum _{i=1}^{n}m_{i}\left(\left[\Delta \mathbf {r} _{i}\right]{\boldsymbol {\omega }}\right)\cdot \left(\left[\Delta \mathbf {r} _{i}\right]{\boldsymbol {\omega }}\right)\right)+{\frac {1}{2}}\left(\sum _{i=1}^{n}m_{i}\right)\mathbf {V} _{\mathbf {C} }\cdot \mathbf {V} _{\mathbf {C} }\\&={\frac {1}{2}}\left(\sum _{i=1}^{n}m_{i}\left({\boldsymbol {\omega }}^{\mathsf {T}}\left[\Delta \mathbf {r} _{i}\right]^{\mathsf {T}}\left[\Delta \mathbf {r} _{i}\right]{\boldsymbol {\omega }}\right)\right)+{\frac {1}{2}}\left(\sum _{i=1}^{n}m_{i}\right)\mathbf {V} _{\mathbf {C} }\cdot \mathbf {V} _{\mathbf {C} }\\&={\frac {1}{2}}{\boldsymbol {\omega }}\cdot \left(-\sum _{i=1}^{n}m_{i}\left[\Delta \mathbf {r} _{i}\right]^{2}\right){\boldsymbol {\omega }}+{\frac {1}{2}}\left(\sum _{i=1}^{n}m_{i}\right)\mathbf {V} _{\mathbf {C} }\cdot \mathbf {V} _{\mathbf {C} }.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c246c5646e149b67a600084c164f154ec7dda89)
Thus, the kinetic energy of the rigid system of particles is given by
Resultant torque
![{\displaystyle \left[\Delta \mathbf {r} _{i}\right]=\left[\mathbf {r} _{i}-\mathbf {C} \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b83ab9af0efe0f59204a493b10b5eb453594c19)
![{\displaystyle {\boldsymbol {\tau }}=\left(-\sum _{i=1}^{n}m_{i}\left[\Delta \mathbf {r} _{i}\right]^{2}\right){\boldsymbol {\alpha }}+{\boldsymbol {\omega }}\times \left(-\sum _{i=1}^{n}m_{i}\left[\Delta \mathbf {r} _{i}\right]^{2}\right){\boldsymbol {\omega }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b93d7ec560fb15fbaaba36a2fd0869da807fd92e)
The calculation uses the identity
obtained from the Jacobi identity for the triple cross product as shown in the proof below:
| Proof |
|---|
| Then, the followingJacobi identityis used on the last term: |
![{\displaystyle {\begin{aligned}{\boldsymbol {\tau }}&=\sum _{i=1}^{n}(\mathbf {r_{i}} -\mathbf {R} )\times (m_{i}\mathbf {a} _{i})\\&=\sum _{i=1}^{n}{\boldsymbol {\Delta }}\mathbf {r} _{i}\times (m_{i}\mathbf {a} _{i})\\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times \mathbf {a} _{i}]\;\ldots {\text{ cross-product scalar multiplication}}\\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times (\mathbf {a} _{{\text{tangential}},i}+\mathbf {a} _{{\text{centripetal}},i}+\mathbf {A} _{\mathbf {R} })]\\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times (\mathbf {a} _{{\text{tangential}},i}+\mathbf {a} _{{\text{centripetal}},i}+0)]\\&\;\;\;\;\;\ldots \;\mathbf {R} {\text{ is either at rest or moving at a constant velocity but not accelerated, or }}\\&\;\;\;\;\;\;\;\;\;\;\;{\text{the origin of the fixed (world) coordinate reference system is placed at the center of mass }}\mathbf {C} \\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times \mathbf {a} _{{\text{tangential}},i}+{\boldsymbol {\Delta }}\mathbf {r} _{i}\times \mathbf {a} _{{\text{centripetal}},i}]\;\ldots {\text{ cross-product distributivity over addition}}\\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\alpha }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\omega }}\times \mathbf {v} _{{\text{tangential}},i})]\\{\boldsymbol {\tau }}&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\alpha }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i}))]\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a1a1b0804a6cf8a550a81732385fca1083051df)
![{\displaystyle {\begin{aligned}0&={\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i}))+{\boldsymbol {\omega }}\times (({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})\times ({\boldsymbol {\Delta }}\mathbf {r} _{i}\times {\boldsymbol {\omega }})\\&={\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i}))+{\boldsymbol {\omega }}\times (({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})\times -({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})\;\ldots {\text{ cross-product anticommutativity}}\\&={\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i}))+{\boldsymbol {\omega }}\times (({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+-[({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})\times ({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})]\;\ldots {\text{ cross-product scalar multiplication}}\\&={\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i}))+{\boldsymbol {\omega }}\times (({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+-[0]\;\ldots {\text{ self cross-product}}\\0&={\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i}))+{\boldsymbol {\omega }}\times (({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})\times {\boldsymbol {\Delta }}\mathbf {r} _{i})\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88ab33d54b34674092a14d55c8ccefb765a2e7ae)
![{\displaystyle {\begin{aligned}{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i}))&=-[{\boldsymbol {\omega }}\times (({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})\times {\boldsymbol {\Delta }}\mathbf {r} _{i})]\\&=-[({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})({\boldsymbol {\omega }}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})-{\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\omega }}\cdot ({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i}))]\;\ldots {\text{ vector triple product}}\\&=-[({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})({\boldsymbol {\omega }}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})-{\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot ({\boldsymbol {\omega }}\times {\boldsymbol {\omega }}))]\;\ldots {\text{ scalar triple product}}\\&=-[({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})({\boldsymbol {\omega }}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})-{\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot (0))]\;\ldots {\text{ self cross-product}}\\&=-[({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})({\boldsymbol {\omega }}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})]\\&=-[{\boldsymbol {\omega }}\times ({\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\omega }}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i}))]\;\ldots {\text{ cross-product scalar multiplication}}\\&={\boldsymbol {\omega }}\times -({\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\omega }}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i}))\;\ldots {\text{ cross-product scalar multiplication}}\\{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i}))&={\boldsymbol {\omega }}\times -({\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\omega }}))\;\ldots {\text{ dot-product commutativity}}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb1ab7d45bf04c0df3101e84282bc6695ddecf68)
![{\displaystyle {\begin{aligned}{\boldsymbol {\tau }}&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\alpha }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i}))]\\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\alpha }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+{\boldsymbol {\omega }}\times -({\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\omega }}))]\\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\alpha }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+{\boldsymbol {\omega }}\times \{0-{\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\omega }})\}]\\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\alpha }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+{\boldsymbol {\omega }}\times \{[{\boldsymbol {\omega }}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})-{\boldsymbol {\omega }}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})]-{\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\omega }})\}]\;\ldots \;{\boldsymbol {\omega }}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})-{\boldsymbol {\omega }}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})=0\\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\alpha }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+{\boldsymbol {\omega }}\times \{[{\boldsymbol {\omega }}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})-{\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\omega }})]-{\boldsymbol {\omega }}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})\}]\;\ldots {\text{ addition associativity}}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66f6f583aacfd008f43218fc24e97547511a6a91)
![{\displaystyle {\begin{aligned}\quad \quad &=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\alpha }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+{\boldsymbol {\omega }}\times \{{\boldsymbol {\omega }}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})-{\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\omega }})\}-{\boldsymbol {\omega }}\times {\boldsymbol {\omega }}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})]\;\ldots {\text{ cross-product distributivity over addition}}\\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\alpha }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+{\boldsymbol {\omega }}\times \{{\boldsymbol {\omega }}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})-{\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\omega }})\}-({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})({\boldsymbol {\omega }}\times {\boldsymbol {\omega }})]\;\ldots {\text{ cross-product scalar multiplication}}\\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\alpha }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+{\boldsymbol {\omega }}\times \{{\boldsymbol {\omega }}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})-{\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\omega }})\}-({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})(0)]\;\ldots {\text{ self cross-product}}\\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\alpha }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+{\boldsymbol {\omega }}\times \{{\boldsymbol {\omega }}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})-{\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\omega }})\}]\\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\alpha }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+{\boldsymbol {\omega }}\times \{{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})\}]\;\ldots {\text{ vector triple product}}\\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times -({\boldsymbol {\Delta }}\mathbf {r} _{i}\times {\boldsymbol {\alpha }})+{\boldsymbol {\omega }}\times \{{\boldsymbol {\Delta }}\mathbf {r} _{i}\times -({\boldsymbol {\Delta }}\mathbf {r} _{i}\times {\boldsymbol {\omega }})\}]\;\ldots {\text{ cross-product anticommutativity}}\\&=-\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\Delta }}\mathbf {r} _{i}\times {\boldsymbol {\alpha }})+{\boldsymbol {\omega }}\times \{{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\Delta }}\mathbf {r} _{i}\times {\boldsymbol {\omega }})\}]\;\ldots {\text{ cross-product scalar multiplication}}\\&=-\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\Delta }}\mathbf {r} _{i}\times {\boldsymbol {\alpha }})]+-\sum _{i=1}^{n}m_{i}[{\boldsymbol {\omega }}\times \{{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\Delta }}\mathbf {r} _{i}\times {\boldsymbol {\omega }})\}]\;\ldots {\text{ summation distributivity}}\\{\boldsymbol {\tau }}&=-\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\Delta }}\mathbf {r} _{i}\times {\boldsymbol {\alpha }})]+{\boldsymbol {\omega }}\times -\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\Delta }}\mathbf {r} _{i}\times {\boldsymbol {\omega }})]\;\ldots \;{\boldsymbol {\omega }}{\text{ is not characteristic of particle }}P_{i}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e44110cbfa3781116aed88aae514e421aa0ca16)
![{\displaystyle {\begin{aligned}-\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\Delta }}\mathbf {r} _{i}\times \mathbf {u} )]&=-\sum _{i=1}^{n}m_{i}\left({\begin{bmatrix}0&-\Delta r_{3,i}&\Delta r_{2,i}\\\Delta r_{3,i}&0&-\Delta r_{1,i}\\-\Delta r_{2,i}&\Delta r_{1,i}&0\end{bmatrix}}\left({\begin{bmatrix}0&-\Delta r_{3,i}&\Delta r_{2,i}\\\Delta r_{3,i}&0&-\Delta r_{1,i}\\-\Delta r_{2,i}&\Delta r_{1,i}&0\end{bmatrix}}{\begin{bmatrix}u_{1}\\u_{2}\\u_{3}\end{bmatrix}}\right)\right)\;\ldots {\text{ cross-product as matrix multiplication}}\\[6pt]&=-\sum _{i=1}^{n}m_{i}\left({\begin{bmatrix}0&-\Delta r_{3,i}&\Delta r_{2,i}\\\Delta r_{3,i}&0&-\Delta r_{1,i}\\-\Delta r_{2,i}&\Delta r_{1,i}&0\end{bmatrix}}{\begin{bmatrix}-\Delta r_{3,i}\,u_{2}+\Delta r_{2,i}\,u_{3}\\+\Delta r_{3,i}\,u_{1}-\Delta r_{1,i}\,u_{3}\\-\Delta r_{2,i}\,u_{1}+\Delta r_{1,i}\,u_{2}\end{bmatrix}}\right)\\[6pt]&=-\sum _{i=1}^{n}m_{i}{\begin{bmatrix}-\Delta r_{3,i}(+\Delta r_{3,i}\,u_{1}-\Delta r_{1,i}\,u_{3})+\Delta r_{2,i}(-\Delta r_{2,i}\,u_{1}+\Delta r_{1,i}\,u_{2})\\+\Delta r_{3,i}(-\Delta r_{3,i}\,u_{2}+\Delta r_{2,i}\,u_{3})-\Delta r_{1,i}(-\Delta r_{2,i}\,u_{1}+\Delta r_{1,i}\,u_{2})\\-\Delta r_{2,i}(-\Delta r_{3,i}\,u_{2}+\Delta r_{2,i}\,u_{3})+\Delta r_{1,i}(+\Delta r_{3,i}\,u_{1}-\Delta r_{1,i}\,u_{3})\end{bmatrix}}\\[6pt]&=-\sum _{i=1}^{n}m_{i}{\begin{bmatrix}-\Delta r_{3,i}^{2}\,u_{1}+\Delta r_{1,i}\Delta r_{3,i}\,u_{3}-\Delta r_{2,i}^{2}\,u_{1}+\Delta r_{1,i}\Delta r_{2,i}\,u_{2}\\-\Delta r_{3,i}^{2}\,u_{2}+\Delta r_{2,i}\Delta r_{3,i}\,u_{3}+\Delta r_{2,i}\Delta r_{1,i}\,u_{1}-\Delta r_{1,i}^{2}\,u_{2}\\+\Delta r_{3,i}\Delta r_{2,i}\,u_{2}-\Delta r_{2,i}^{2}\,u_{3}+\Delta r_{3,i}\Delta r_{1,i}\,u_{1}-\Delta r_{1,i}^{2}\,u_{3}\end{bmatrix}}\\[6pt]&=-\sum _{i=1}^{n}m_{i}{\begin{bmatrix}-(\Delta r_{2,i}^{2}+\Delta r_{3,i}^{2})\,u_{1}+\Delta r_{1,i}\Delta r_{2,i}\,u_{2}+\Delta r_{1,i}\Delta r_{3,i}\,u_{3}\\+\Delta r_{2,i}\Delta r_{1,i}\,u_{1}-(\Delta r_{1,i}^{2}+\Delta r_{3,i}^{2})\,u_{2}+\Delta r_{2,i}\Delta r_{3,i}\,u_{3}\\+\Delta r_{3,i}\Delta r_{1,i}\,u_{1}+\Delta r_{3,i}\Delta r_{2,i}\,u_{2}-(\Delta r_{1,i}^{2}+\Delta r_{2,i}^{2})\,u_{3}\end{bmatrix}}\\[6pt]&=-\sum _{i=1}^{n}m_{i}{\begin{bmatrix}-(\Delta r_{2,i}^{2}+\Delta r_{3,i}^{2})&\Delta r_{1,i}\Delta r_{2,i}&\Delta r_{1,i}\Delta r_{3,i}\\\Delta r_{2,i}\Delta r_{1,i}&-(\Delta r_{1,i}^{2}+\Delta r_{3,i}^{2})&\Delta r_{2,i}\Delta r_{3,i}\\\Delta r_{3,i}\Delta r_{1,i}&\Delta r_{3,i}\Delta r_{2,i}&-(\Delta r_{1,i}^{2}+\Delta r_{2,i}^{2})\end{bmatrix}}{\begin{bmatrix}u_{1}\\u_{2}\\u_{3}\end{bmatrix}}\\&=-\sum _{i=1}^{n}m_{i}[\Delta r_{i}]^{2}\mathbf {u} \\[6pt]-\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\Delta }}\mathbf {r} _{i}\times \mathbf {u} )]&=\left(-\sum _{i=1}^{n}m_{i}[\Delta r_{i}]^{2}\right)\mathbf {u} \;\ldots \;\mathbf {u} {\text{ is not characteristic of }}P_{i}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/059812b4501e0672712b5b7adff834e79c3b4bff)
![{\displaystyle {\begin{aligned}{\boldsymbol {\tau }}&=-\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\Delta }}\mathbf {r} _{i}\times {\boldsymbol {\alpha }})]+{\boldsymbol {\omega }}\times -\sum _{i=1}^{n}m_{i}{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\Delta }}\mathbf {r} _{i}\times {\boldsymbol {\omega }})]\\&=\left(-\sum _{i=1}^{n}m_{i}[\Delta r_{i}]^{2}\right){\boldsymbol {\alpha }}+{\boldsymbol {\omega }}\times \left(-\sum _{i=1}^{n}m_{i}[\Delta r_{i}]^{2}\right){\boldsymbol {\omega }}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0971bbc71e7ceb3c810afa1043b08aca54608486)
Thus, the resultant torque on the rigid system of particles is given by
Parallel axis theorem
![{\displaystyle \mathbf {I} _{\mathbf {R} }=-\sum _{i=1}^{n}m_{i}\left[\mathbf {r} _{i}-\mathbf {R} \right]^{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93e62233b3acff4fc919fc24e8d6241551543087)
![{\displaystyle \mathbf {I} _{\mathbf {R} }=-\sum _{i=1}^{n}m_{i}[\mathbf {r} _{i}-\left(\mathbf {C} +\mathbf {d} \right)]^{2}=-\sum _{i=1}^{n}m_{i}[\left(\mathbf {r} _{i}-\mathbf {C} \right)-\mathbf {d} ]^{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0063409d605348215928372e62f294287f06fb98)
Distribute over the cross product to obtain
![{\displaystyle \mathbf {I} _{\mathbf {R} }=-\left(\sum _{i=1}^{n}m_{i}[\mathbf {r} _{i}-\mathbf {C} ]^{2}\right)+\left(\sum _{i=1}^{n}m_{i}[\mathbf {r} _{i}-\mathbf {C} ]\right)[\mathbf {d} ]+[\mathbf {d} ]\left(\sum _{i=1}^{n}m_{i}[\mathbf {r} _{i}-\mathbf {C} ]\right)-\left(\sum _{i=1}^{n}m_{i}\right)[\mathbf {d} ]^{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68eee7fefe0e716823fd5d80384303b8aef58b99)
![{\displaystyle [\mathbf {d} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5785dcf9605fb6ace7c1a8c8b4d6b365af48366)
The result is the parallel axis theorem,
![{\displaystyle \mathbf {I} _{\mathbf {R} }=\mathbf {I} _{\mathbf {C} }-M[\mathbf {d} ]^{2},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c59b0848c4b1d69fff75c4257005225cd42c74d)
![{\displaystyle -m\left[\mathbf {r} \right]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b3ed54432828b43d6ae23e9a2e9c009c7336024)
![{\displaystyle m\left[\mathbf {r} \right]^{\mathsf {T}}\left[\mathbf {r} \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/27fed5e06e85cd3d74847c333b7a32cbd6a31fe7)
![{\displaystyle [\mathbf {r} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba4c4e0b7a62e35392117d1331b60c9e3276b5c9)
Scalar moment of inertia in a plane
![{\displaystyle I_{L}=\mathbf {\hat {k}} \cdot \left(-\sum _{i=1}^{N}m_{i}\left[\Delta \mathbf {r} _{i}\right]^{2}\right)\mathbf {\hat {k}} =\mathbf {\hat {k}} \cdot \mathbf {I} _{\mathbf {R} }\mathbf {\hat {k}} =\mathbf {\hat {k}} ^{\mathsf {T}}\mathbf {I} _{\mathbf {R} }\mathbf {\hat {k}} ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78bb7c062959fd615347939341b32bf66de221c6)
![{\displaystyle \left[\mathbf {\hat {k}} \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a515c7495954477be07dee4f29d4c4c4ec50cf98)
![{\displaystyle \left[\mathbf {\hat {k}} \right]\mathbf {y} =\mathbf {\hat {k}} \times \mathbf {y} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/10d1281a399f50084c4d71e516f5d56b1cf5426f)
![{\displaystyle -\left[\mathbf {\hat {k}} \right]^{2}\equiv \left|\mathbf {\hat {k}} \right|^{2}\left(\mathbf {E} -\mathbf {\hat {k}} \mathbf {\hat {k}} ^{\mathsf {T}}\right)=\mathbf {E} -\mathbf {\hat {k}} \mathbf {\hat {k}} ^{\mathsf {T}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d92be0b3adbb50fbe61b31dc0237f0fc102476a0)
The magnitude squared of the perpendicular vector is
![{\displaystyle {\begin{aligned}\left|\Delta \mathbf {r} _{i}^{\perp }\right|^{2}&=\left(-\left[\mathbf {\hat {k}} \right]^{2}\Delta \mathbf {r} _{i}\right)\cdot \left(-\left[\mathbf {\hat {k}} \right]^{2}\Delta \mathbf {r} _{i}\right)\\&=\left(\mathbf {\hat {k}} \times \left(\mathbf {\hat {k}} \times \Delta \mathbf {r} _{i}\right)\right)\cdot \left(\mathbf {\hat {k}} \times \left(\mathbf {\hat {k}} \times \Delta \mathbf {r} _{i}\right)\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d205a6da935ecfa8f5e13feb1a930f1d032022a)
The simplification of this equation uses the triple scalar product identity
![{\displaystyle {\begin{aligned}&\left(\mathbf {\hat {k}} \times \left(\mathbf {\hat {k}} \times \Delta \mathbf {r} _{i}\right)\right)\cdot \left(\mathbf {\hat {k}} \times \left(\mathbf {\hat {k}} \times \Delta \mathbf {r} _{i}\right)\right)\\={}&\left(\left(\mathbf {\hat {k}} \times \left(\mathbf {\hat {k}} \times \Delta \mathbf {r} _{i}\right)\right)\times \mathbf {\hat {k}} \right)\cdot \left(\mathbf {\hat {k}} \times \Delta \mathbf {r} _{i}\right)\\={}&\left(\mathbf {\hat {k}} \times \Delta \mathbf {r} _{i}\right)\cdot \left(-\Delta \mathbf {r} _{i}\times \mathbf {\hat {k}} \right)\\={}&-\mathbf {\hat {k}} \cdot \left(\Delta \mathbf {r} _{i}\times \Delta \mathbf {r} _{i}\times \mathbf {\hat {k}} \right)\\={}&-\mathbf {\hat {k}} \cdot \left[\Delta \mathbf {r} _{i}\right]^{2}\mathbf {\hat {k}} .\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62111ff66a6922e2705a7eb60478088077b7d9bf)
![{\displaystyle {\begin{aligned}I_{L}&=\sum _{i=1}^{N}m_{i}\left|\Delta \mathbf {r} _{i}^{\perp }\right|^{2}\\&=-\sum _{i=1}^{N}m_{i}\mathbf {\hat {k}} \cdot \left[\Delta \mathbf {r} _{i}\right]^{2}\mathbf {\hat {k}} =\mathbf {\hat {k}} \cdot \left(-\sum _{i=1}^{N}m_{i}\left[\Delta \mathbf {r} _{i}\right]^{2}\right)\mathbf {\hat {k}} \\&=\mathbf {\hat {k}} \cdot \mathbf {I} _{\mathbf {R} }\mathbf {\hat {k}} =\mathbf {\hat {k}} ^{\mathsf {T}}\mathbf {I} _{\mathbf {R} }\mathbf {\hat {k}} ,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f4a4a61db87467a4b76294e68bba221a2810cdf)
This shows that the inertia matrix can be used to calculate the moment of inertia of a body around any specified rotation axis in the body.
Inertia tensor
For the same object, different axes of rotation will have different moments of inertia about those axes. In general, the moments of inertia are not equal unless the object is symmetric about all axes. The moment of inertia tensor is a convenient way to summarize all moments of inertia of an object with one quantity. It may be calculated with respect to any point in space, although for practical purposes the center of mass is most commonly used.
Definition
- .
Its components are defined as
where
- i, j equal 1, 2, or 3 for x, y, and z, respectively,r=(x1, x2, x3) is the vector to the mass element dm from the point about which the tensor is calculated, r=||x||, and
- is the
Note that, by the definition, I is a symmetric tensor.
The diagonal elements, also called the principal moments of inertia, are more succinctly written as
while the off-diagonal elements, also called the products of inertia, are
- and
These quantities can be generalized to an object with distributed mass, described by a mass density function, in a similar fashion to the scalar moment of inertia. One then has
![{\displaystyle [\mathbf {r} ]\mathbf {x} =\mathbf {r} \times \mathbf {x} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f32ba1c18fa5966e4dcd2275a7f7e3bc21f6dc0)
![{\displaystyle \mathbf {I} =\iiint \limits _{V}\rho (\mathbf {r} )[\mathbf {r} ]^{T}[\mathbf {r} ]\,\mathrm {d} V=-\iiint \limits _{Q}\rho (\mathbf {r} )[\mathbf {r} ]^{2}\,\mathrm {d} V}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f40ecc4afdc8348d26190e66f88ffd2d5f12c16e)
The components of tensors of degree two can be assembled into a matrix. For the inertia tensor this matrix is given by,
Derivation of the tensor components
- .
![{\displaystyle {I}=m[n_{1},n_{2},n_{3}]{\begin{bmatrix}y^{2}+z^{2}&-xy&-xz\\-yx&x^{2}+z^{2}&-yz\\-zx&-zy&x^{2}+y^{2}\end{bmatrix}}{\begin{bmatrix}n_{1}\\n_{2}\\n_{3}\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78853d5e6150e6711193d1a033018a59151aac6a)
For multiple particles we need only recall that the moment of inertia is additive in order to see that this formula is correct.
Inertia matrix in different reference frames
The use of the inertia matrix in Newton's second law assumes its components are computed relative to axes parallel to the inertial frame and not relative to a body-fixed reference frame.[6][23] This means that as the body moves the components of the inertia matrix change with time. In contrast, the components of the inertia matrix measured in a body-fixed frame are constant.
Body frame
Principal axes
where
When all principal moments of inertia are distinct, the principal axes through center of mass are uniquely specified. If two principal moments are the same, the rigid body is called a symmetrical top and there is no unique choice for the two corresponding principal axes. If all three principal moments are the same, the rigid body is called a spherical top (although it need not be spherical) and any axis can be considered a principal axis, meaning that the moment of inertia is the same about any axis.
The motion of vehicles is often described in terms of yaw, pitch, and roll which usually correspond approximately to rotations about the three principal axes. If the vehicle has bilateral symmetry then one of the principal axes will correspond exactly to the transverse (pitch) axis.
A practical example of this mathematical phenomenon is the routine automotive task of balancing a tire, which basically means adjusting the distribution of mass of a car wheel such that its principal axis of inertia is aligned with the axle so the wheel does not wobble.
Ellipsoid
An ellipsoid with the semi-principal diameters labelled , , and .
or
defines an ellipsoid in the body frame. Write this equation in the form,
to see that the semi-principal diameters of this ellipsoid are given by
See also
Central moment
List of moments of inertia
Rotational energy