Maxwell–Boltzmann distribution
Maxwell–Boltzmann distribution
In physics (in particular in statistical mechanics), the Maxwell–Boltzmann distribution is a particular probability distribution named after James Clerk Maxwell and Ludwig Boltzmann.
It was first defined and used for describing particle speeds in idealized gases, where the particles move freely inside a stationary container without interacting with one another, except for very brief collisions in which they exchange energy and momentum with each other or with their thermal environment. The term "particle" in this context refers to gaseous particles only (atoms or molecules), and the system of particles is assumed to have reached thermodynamic equilibrium.[1] The energies of such particles follow what is known as Maxwell-Boltzmann statistics, and the statistical distribution of speeds is derived by equating particle energies with kinetic energy.
The Maxwell–Boltzmann distribution is a result of the kinetic theory of gases, which provides a simplified explanation of many fundamental gaseous properties, including pressure and diffusion.[3] The Maxwell–Boltzmann distribution applies fundamentally to particle velocities in three dimensions, but turns out to depend only on the speed (the magnitude of the velocity) of the particles. A particle speed probability distribution indicates which speeds are more likely: a particle will have a speed selected randomly from the distribution, and is more likely to be within one range of speeds than another. The kinetic theory of gases applies to the classical ideal gas, which is an idealization of real gases. In real gases, there are various effects (e.g., van der Waals interactions, vortical flow, relativistic speed limits, and quantum exchange interactions) that can make their speed distribution different from the Maxwell–Boltzmann form. However, rarefied gases at ordinary temperatures behave very nearly like an ideal gas and the Maxwell speed distribution is an excellent approximation for such gases. Ideal plasmas, which are ionized gases of sufficiently low density, frequently also have particle distributions that are partially or entirely Maxwellian.[4]
The distribution was first derived by Maxwell in 1860 on heuristic grounds.[5] Boltzmann later, in the 1870s, carried out significant investigations into the physical origins of this distribution.
The distribution can be derived on the ground that it maximizes the entropy of the system. A list of derivations are:
Maximum entropy probability distribution in the phase space, with the constraint of Conservation of average energy ;
Canonical ensemble.
Distribution function
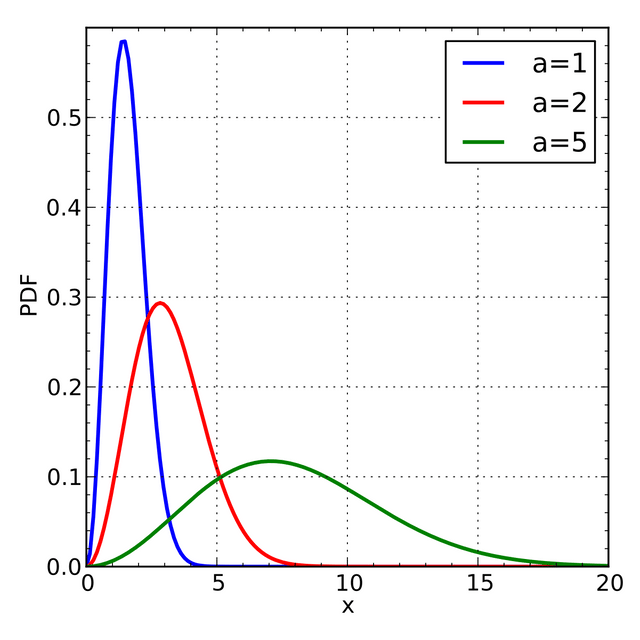
The speed probability density functions of the speeds of a few noble gases at a temperature of 298.15 K (25 °C). The y-axis is in s/m so that the area under any section of the curve (which represents the probability of the speed being in that range) is dimensionless.
The simplest ordinary differential equation satisfied by the distribution is:
or in unitless presentation:
With the Darwin–Fowler method of mean values the Maxwell–Boltzmann distribution is obtained as an exact result.
Relaxation to the 2D Maxwell-Boltzmann distribution
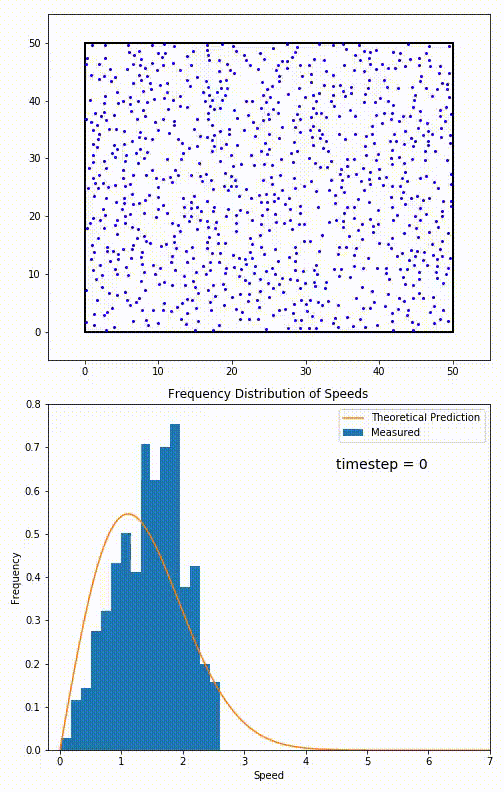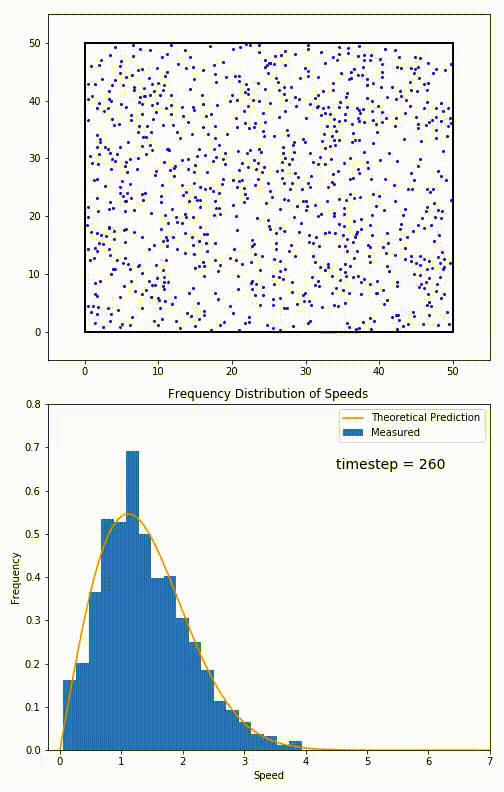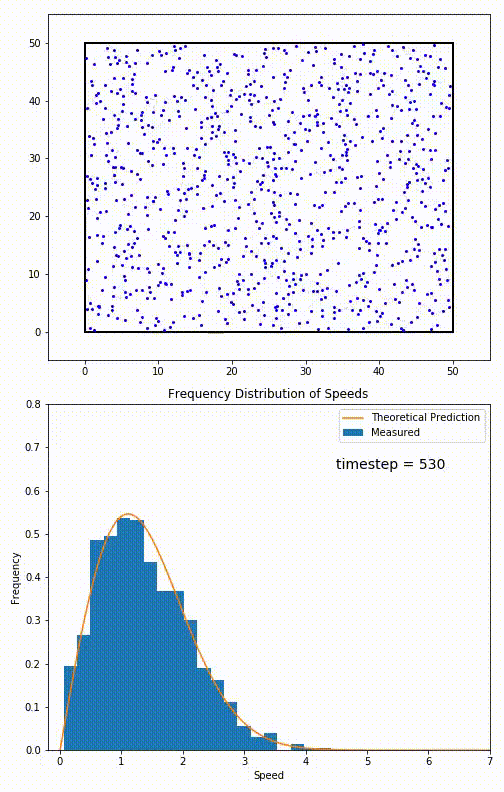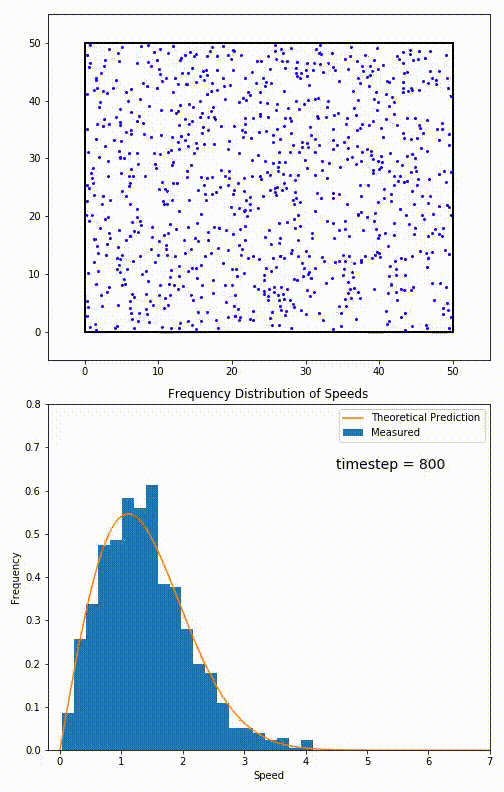
Simulation of a 2D gas relaxing towards a Maxwell-Boltzmann speed distribution
For particles confined to move in a plane, the speed distribution is given by
This distribution is used for describing systems in equilibrium. However, most systems do start out in their equilibrium state. The evolution of a system towards its equilibrium state is governed by the Boltzmann equation. The equation predicts that for short range interactions, the equilibrium velocity distribution will follow a Maxwell–Boltzmann distribution. To the right is a molecular dynamics (MD) simulation in which 900 hard sphere particles are constrained to move in a rectangle. They interact via perfectly elastic collisions. The system is initialized out of equilibrium, but we see that the velocity distribution (in blue) quickly converges to the 2D Maxwell–Boltzmann distribution (in orange).
Typical speeds
This works well for nearly ideal, monatomic gases like helium, but also for molecular gases like diatomic oxygen. This is because despite the larger heat capacity (larger internal energy at the same temperature) due to their larger number of degrees of freedom, their translational kinetic energy (and thus their speed) is unchanged.[7]
In summary, the typical speeds are related as follows:
The root mean square speed is directly related to the speed of sound c in the gas, by
the true value for air can be approximated by using the average molar weight of air (29 g/mol), yielding 347 m/s at 300 K (corrections for variable humidity are of the order of 0.1% to 0.6%).
The average relative velocity
where the three-dimensional velocity distribution is
Derivation and related distributions
Maxwell–Boltzmann statistics
The original derivation in 1860 by James Clerk Maxwell was an argument based on molecular collisions of the Kinetic theory of gases as well as certain symmetries in the speed distribution function; Maxwell also gave an early argument that these molecular collisions entail a tendency towards equilibrium.[5][10] After Maxwell, Ludwig Boltzmann in 1872[11] also derived the distribution on mechanical grounds and argued that gases should over time tend toward this distribution, due to collisions (see H-theorem). He later (1877)[12] derived the distribution again under the framework of statistical thermodynamics. The derivations in this section are along the lines of Boltzmann's 1877 derivation, starting with result known as Maxwell–Boltzmann statistics (from statistical thermodynamics). Maxwell–Boltzmann statistics gives the average number of particles found in a given single-particle microstate. Under certain assumptions, the logarithm of the fraction of particles in a given microstate is proportional to the ratio of the energy of that state to the temperature of the system:
This relation can be written as an equation by introducing a normalizing factor:
| **(1)** |
where:
Ni is the expected number of particles in the single-particle microstate i,
N is the total number of particles in the system,
Ei is the energy of microstate i,
the sum over index j takes into account all microstates,
T is the equilibrium temperature of the system,
k is the Boltzmann constant.
Because velocity and speed are related to energy, Equation (1) can be used to derive relationships between temperature and the speeds of gas particles. All that is needed is to discover the density of microstates in energy, which is determined by dividing up momentum space into equal sized regions.
Distribution for the momentum vector
The potential energy is taken to be zero, so that all energy is in the form of kinetic energy. The relationship between kinetic energy and momentum for massive non-relativistic particles is
| **(2)** |
where p2 is the square of the momentum vector p = [p**x, p**y, p**z]. We may therefore rewrite Equation (1) as:
| **(3)** |
![\frac{N_i}{N} =
\frac{1}{Z}
\exp \left[
-\frac{p_{i, x}^2 + p_{i, y}^2 + p_{i, z}^2}{2mkT}
\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/8dc173ee0113a100c4713d64801c5f4d028cff71)
| **(4)** |
![{\displaystyle f_{\mathbf {p} }(p_{x},p_{y},p_{z})\propto \exp \left[-{\frac {p_{x}^{2}+p_{y}^{2}+p_{z}^{2}}{2mkT}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3712e79fe2355995f5c9ee99a51c83127dff8a0a)
The normalizing constant can be determined by recognizing that the probability of a molecule having some momentum must be 1.
Integrating the exponential in (4) over all p**x, p**y, and p**z yields a factor of
![{\displaystyle \iiint _{-\infty }^{+\infty }\exp \left[-{\frac {p_{x}^{2}+p_{y}^{2}+p_{z}^{2}}{2mkT}}\right]dp_{x}\ dp_{y}\ dp_{z}={({\sqrt {\pi }}{\sqrt {2mkT}})^{3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/70f4955201fb75e0921b1738f340ca8d935c95b6)
So that the normalized distribution function is:
Distribution for the energy
The energy distribution is found imposing
| **(7)** |
| **(8)** |
and finally
Since the energy is proportional to the sum of the squares of the three normally distributed momentum components, this distribution is a gamma distribution; in particular, it is a chi-squared distribution with three degrees of freedom.
By the equipartition theorem, this energy is evenly distributed among all three degrees of freedom, so that the energy per degree of freedom is distributed as a chi-squared distribution with one degree of freedom:[14]
![{\displaystyle f_{\epsilon }(\epsilon )\,d\epsilon ={\sqrt {\frac {1}{\pi \epsilon kT}}}~\exp \left[{\frac {-\epsilon }{kT}}\right]\,d\epsilon }](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d0b957722f14b4f35ca02434218927e2ffff4d4)
The Maxwell–Boltzmann distribution can also be obtained by considering the gas to be a type of quantum gas for which the approximation ε >> k T may be made.
Distribution for the velocity vector
Recognizing that the velocity probability density fv is proportional to the momentum probability density function by
and using p = mv we get
which is the Maxwell–Boltzmann velocity distribution. The probability of finding a particle with velocity in the infinitesimal element [dv**x, dv**y, dv**z] about velocity v = [v**x, v**y, v**z] is
where the distribution for a single direction is
![f_v (v_i) =
\sqrt{\frac{m}{2 \pi kT}}
\exp \left[
\frac{-mv_i^2}{2kT}
\right].](https://wikimedia.org/api/rest_v1/media/math/render/svg/86a6d2151bda2079488be11059d0320477fb8eb8)
Distribution for the speed
The Maxwell–Boltzmann distribution for the speed follows immediately from the distribution of the velocity vector, above. Note that the speed is
and the volume element in spherical coordinates
In n-dimensional space
In n-dimensional space, Maxwell-Boltzman distribution becomes:
Speed distribution becomes:
The following integral result is useful:
![{\displaystyle {\begin{aligned}\int _{0}^{+\infty }v^{a}e^{-{\frac {mv^{2}}{2kT}}}dv&=\left[{\frac {2kT}{m}}\right]^{(a+1)/2}\int _{0}^{+\infty }e^{-x}x^{\frac {a}{2}}dx^{\frac {1}{2}}\\&=\left[{\frac {2kT}{m}}\right]^{(a+1)/2}\int _{0}^{+\infty }e^{-x}x^{\frac {a}{2}}{\frac {x^{-{\frac {1}{2}}}}{2}}dx\\&=\left[{\frac {2kT}{m}}\right]^{(a+1)/2}{\frac {\Gamma ({\frac {a+1}{2}})}{2}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5aa880a767dda0a1e61815cab2be0c852f49e72)
![{\displaystyle {\begin{aligned}\langle v\rangle &={\frac {\int _{0}^{+\infty }v\cdot v^{n-1}e^{-{\frac {mv^{2}}{2kT}}}dv}{\int _{0}^{+\infty }v^{n-1}e^{-{\frac {mv^{2}}{2kT}}}dv}}\\&=\left[{\frac {2kT}{m}}\right]^{1/2}{\frac {\Gamma ({\frac {n+1}{2}})}{\Gamma ({\frac {n}{2}})}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c2b85e7ed2894cbdb61eb8583ebfbe02d526b97)
![{\displaystyle v_{\text{avg}}=\langle v\rangle =\left[{\frac {2kT}{m}}\right]^{1/2}{\frac {\Gamma ({\frac {n+1}{2}})}{\Gamma ({\frac {n}{2}})}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8505a8edd15b531a592698dbcbe9f8f52ea34575)
![{\displaystyle {\begin{aligned}\langle v^{2}\rangle &={\frac {\int _{0}^{+\infty }v^{2}\cdot v^{n-1}e^{-{\frac {mv^{2}}{2kT}}}dv}{\int _{0}^{+\infty }v^{n-1}e^{-{\frac {mv^{2}}{2kT}}}dv}}\\&=\left[{\frac {2kT}{m}}\right]{\frac {\Gamma ({\frac {n+2}{2}})}{\Gamma ({\frac {n}{2}})}}\\&=\left[{\frac {2kT}{m}}\right]{\frac {n}{2}}={\frac {nkT}{m}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7229babe1109170d8853238e96bbd3ee0087ee56)
![{\displaystyle v_{\text{rms}}={\sqrt {\langle v^{2}\rangle }}=\left[{\frac {nkT}{m}}\right]^{1/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32fda78e6ecf4e6ae459bc6cf9be6079f4696be7)
The derivative of speed distribution function:
![{\displaystyle v_{\text{p}}=\left[{\frac {(n-1)kT}{m}}\right]^{1/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b44dc8c0dac800d391af84f1db820e64c44c21b)
See also
Quantum Boltzmann equation
Maxwell–Jüttner distribution
Boltzmann distribution
Boltzmann factor
Rayleigh distribution