Euler–Bernoulli beam theory

Euler–Bernoulli beam theory

Euler–Bernoulli beam theory (also known as engineer's beam theory or classical beam theory)[2] is a simplification of the linear theory of elasticity which provides a means of calculating the load-carrying and deflection characteristics of beams. It covers the case for small deflections of a beam that are subjected to lateral loads only. It is thus a special case of Timoshenko beam theory. It was first enunciated circa 1750,[3] but was not applied on a large scale until the development of the Eiffel Tower and the Ferris wheel in the late 19th century. Following these successful demonstrations, it quickly became a cornerstone of engineering and an enabler of the Second Industrial Revolution.
Additional analysis tools have been developed such as plate theory and finite element analysis, but the simplicity of beam theory makes it an important tool in the sciences, especially structural and mechanical engineering.
History
Prevailing consensus is that Galileo Galilei made the first attempts at developing a theory of beams, but recent studies argue that Leonardo da Vinci was the first to make the crucial observations. Da Vinci lacked Hooke's law and calculus to complete the theory, whereas Galileo was held back by an incorrect assumption he made.[4]
The Bernoulli beam is named after Jacob Bernoulli, who made the significant discoveries. Leonhard Euler and Daniel Bernoulli were the first to put together a useful theory circa 1750.[5] At the time, science and engineering were generally seen as very distinct fields, and there was considerable doubt that a mathematical product of academia could be trusted for practical safety applications. Bridges and buildings continued to be designed by precedent until the late 19th century, when the Eiffel Tower and Ferris wheel demonstrated the validity of the theory on large scales.
Static beam equation
The Euler–Bernoulli equation describes the relationship between the beam's deflection and the applied load:[6]

 describes the deflection of the beam in the
describes the deflection of the beam in the direction at some position
direction at some position (recall that the beam is modeled as a one-dimensional object).
(recall that the beam is modeled as a one-dimensional object). is a distributed load, in other words a force per unit length (analogous topressurebeing a force per area); it may be a function of
is a distributed load, in other words a force per unit length (analogous topressurebeing a force per area); it may be a function of ,
, , or other variables.
, or other variables. is theelastic modulusand
is theelastic modulusand is thesecond moment of areaof the beam's cross-section.
is thesecond moment of areaof the beam's cross-section. must be calculated with respect to the axis which passes through the centroid of the cross-section and which is perpendicular to the applied loading.[1] Explicitly, for a beam whose axis is oriented along x with a loading along z, the beam's cross-section is in the yz plane, and the relevant second moment of area is
must be calculated with respect to the axis which passes through the centroid of the cross-section and which is perpendicular to the applied loading.[1] Explicitly, for a beam whose axis is oriented along x with a loading along z, the beam's cross-section is in the yz plane, and the relevant second moment of area is
where it is assumed that the centroid of the cross-section occurs at y = z = 0.
 (known as theflexural rigidity) is a constant, so that
(known as theflexural rigidity) is a constant, so that
 for common beam configurations can be found in engineering handbooks. For more complicated situations, the deflection can be determined by solving the Euler–Bernoulli equation using techniques such as "direct integration", "Macaulay's method", "moment area method, "conjugate beam method", "the principle of virtual work", "Castigliano's method", "flexibility method", "slope deflection method", "moment distribution method", or "direct stiffness method".
for common beam configurations can be found in engineering handbooks. For more complicated situations, the deflection can be determined by solving the Euler–Bernoulli equation using techniques such as "direct integration", "Macaulay's method", "moment area method, "conjugate beam method", "the principle of virtual work", "Castigliano's method", "flexibility method", "slope deflection method", "moment distribution method", or "direct stiffness method". where
where ,
, , and
, and are unit vectors in the direction of the x, y, and z axes respectively, the y axis direction is into the figure. Forces acting in the positive
are unit vectors in the direction of the x, y, and z axes respectively, the y axis direction is into the figure. Forces acting in the positive and
and directions are assumed positive. The sign of the bending moment
directions are assumed positive. The sign of the bending moment is positive when the torque vector associated with the bending moment on the right hand side of the section is in the positive y direction (i.e. so that a positive value of
is positive when the torque vector associated with the bending moment on the right hand side of the section is in the positive y direction (i.e. so that a positive value of leads to a compressive stress at the bottom fibers). With this choice of bending moment sign convention, in order to have
leads to a compressive stress at the bottom fibers). With this choice of bending moment sign convention, in order to have , it is necessary that the shear force
, it is necessary that the shear force acting on the right side of the section be positive in the z direction so as to achieve static equilibrium of moments. To have force equilibrium with
acting on the right side of the section be positive in the z direction so as to achieve static equilibrium of moments. To have force equilibrium with , the loading intensity
, the loading intensity must be positive in the negative z direction. In addition to these sign conventions for scalar quantities, we also sometimes use vectors in which the directions of the vectors is made clear through the use of the unit vectors,
must be positive in the negative z direction. In addition to these sign conventions for scalar quantities, we also sometimes use vectors in which the directions of the vectors is made clear through the use of the unit vectors, ,
, , and
, and .
. have important physical meanings:
have important physical meanings: is the slope of the beam,
is the slope of the beam,
is the bending moment in the beam, and

is the shear force in the beam.
The stresses in a beam can be calculated from the above expressions after the deflection due to a given load has been determined.
Derivation of bending moment equation
 The length of a fiber with a radial distance
The length of a fiber with a radial distance below the neutral axis is
below the neutral axis is Therefore, the strain of this fiber is
Therefore, the strain of this fiber is
 where
where is theelastic modulusin accordance withHooke's Law. The differential force vector,
is theelastic modulusin accordance withHooke's Law. The differential force vector, resulting from this stress is given by,
resulting from this stress is given by,
 direction since the figure clearly shows that the fibers in the lower half are in tension.
direction since the figure clearly shows that the fibers in the lower half are in tension. is the differential element of area at the location of the fiber. The differential bending moment vector,
is the differential element of area at the location of the fiber. The differential bending moment vector, associated with
associated with is given by
is given by
 Therefore, we integrate over the entire cross section of the beam and get for
Therefore, we integrate over the entire cross section of the beam and get for the bending moment vector exerted on the right cross section of the beam the expression
the bending moment vector exerted on the right cross section of the beam the expression
 is thesecond moment of area. From calculus, we know that when
is thesecond moment of area. From calculus, we know that when is small as it is for an Euler–Bernoulli beam,
is small as it is for an Euler–Bernoulli beam, (
( is theradius of curvature). Therefore,
is theradius of curvature). Therefore,
Dynamic beam equation
The dynamic beam equation is the Euler–Lagrange equation for the following action
![{\displaystyle S=\int _{t_{1}}^{t_{2}}\int _{0}^{L}\left[{\frac {1}{2}}\mu \left({\frac {\partial w}{\partial t}}\right)^{2}-{\frac {1}{2}}EI\left({\frac {\partial ^{2}w}{\partial x^{2}}}\right)^{2}+q(x)w(x,t)\right]dxdt.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/344adbcade0f3dddbc62314c2f884550f7288ec8)
 is the mass per unit length; the second one represents the potential energy due to internal forces (when considered with a negative sign) and the third term represents the potential energy due to the external load
is the mass per unit length; the second one represents the potential energy due to internal forces (when considered with a negative sign) and the third term represents the potential energy due to the external load . TheEuler–Lagrange equationis used to determine the function that minimizes the functional
. TheEuler–Lagrange equationis used to determine the function that minimizes the functional . For a dynamic Euler–Bernoulli beam, the Euler–Lagrange equation is
. For a dynamic Euler–Bernoulli beam, the Euler–Lagrange equation is| Derivation of Euler–Lagrange equation for beams |
|---|
| Since theLagrangianis |
 and
and are independent of
are independent of , and the beam equation is simpler:
, and the beam equation is simpler:
Free vibration
 , we have the free vibration equation. This equation can be solved using a Fourier decomposition of the displacement into the sum of harmonic vibrations of the form
, we have the free vibration equation. This equation can be solved using a Fourier decomposition of the displacement into the sum of harmonic vibrations of the form![w(x,t)={\text{Re}}[{\hat {w}}(x)~e^{{-i\omega t}}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9107e40d745b3d23b0e79b6ee1620bbf6f123cc)
 is the frequency of vibration. Then, for each value of frequency, we can solve an ordinary differential equation
is the frequency of vibration. Then, for each value of frequency, we can solve an ordinary differential equation
The general solution of the above equation is

 are constants. These constants are unique for a given set of boundary conditions. However, the solution for the displacement is not unique and depends on the frequency. These solutions are typically written as
are constants. These constants are unique for a given set of boundary conditions. However, the solution for the displacement is not unique and depends on the frequency. These solutions are typically written as
 are called the natural frequencies of the beam. Each of the displacement solutions is called a mode and the shape of the displacement curve is called the mode shape.
are called the natural frequencies of the beam. Each of the displacement solutions is called a mode and the shape of the displacement curve is called the mode shape.Example: Cantilevered beam
 (fixed at
(fixed at ) are
) are
 This nonlinear equation can be solved numerically. The first few roots are *β1L/π* = 0.59686..., *β2L/π* = 1.49418..., *β3L/π* = 2.50025..., *β4L/π* = 3.49999..., ...
This nonlinear equation can be solved numerically. The first few roots are *β1L/π* = 0.59686..., *β2L/π* = 1.49418..., *β3L/π* = 2.50025..., *β4L/π* = 3.49999..., ...The corresponding natural frequencies of vibration are

The boundary conditions can also be used to determine the mode shapes from the solution for the displacement:
![{\displaystyle {\hat {w}}_{n}=A_{1}{\Bigl [}(\cosh \beta _{n}x-\cos \beta _{n}x)+{\frac {\cos \beta _{n}L+\cosh \beta _{n}L}{\sin \beta _{n}L+\sinh \beta _{n}L}}(\sin \beta _{n}x-\sinh \beta _{n}x){\Bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1eb2d55994ded966b4d7d51484d32b46647cc2a2)
 ),
), , which in general is complex, is determined by the initial conditions at
, which in general is complex, is determined by the initial conditions at on the velocity and displacements of the beam. Typically a value of
on the velocity and displacements of the beam. Typically a value of is used when plotting mode shapes. Solutions to the undampened forced problem have unbounded displacements when the driving frequency matches a natural frequency
is used when plotting mode shapes. Solutions to the undampened forced problem have unbounded displacements when the driving frequency matches a natural frequency , i.e., the beam can resonate. The natural frequencies of a beam therefore correspond to the frequencies at which resonance can occur.
, i.e., the beam can resonate. The natural frequencies of a beam therefore correspond to the frequencies at which resonance can occur.Example: unsupported (free-free) beam
A free-free beam is a beam without any supports.[7] The boundary conditions for a free beam of length L extending from x=0 to x=L is given by:


This nonlinear equation can be solved numerically. The first few roots are β1 L/π = 1.50562..., β2 L/π = 2.49975..., β3 L/π = 3.50001..., β4 L/π = 4.50000...
The corresponding natural frequencies of vibration are:

The boundary conditions can also be used to determine the mode shapes from the solution for the displacement:
![{\displaystyle {\hat {w}}_{n}=A_{1}{\Bigl [}(\sin \beta _{n}x+\sinh \beta _{n}x)+{\frac {\sin \beta _{n}L-\sinh \beta _{n}L}{\cosh \beta _{n}L-\cos \beta _{n}L}}(\cos \beta _{n}x+\cosh \beta _{n}x){\Bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9cf847f2d763cc0b989014a80c9a68994b6c208)
 on the velocity and displacements of the beam. Also, solutions to the undampened forced problem have unbounded displacements when the driving frequency matches a natural frequency
on the velocity and displacements of the beam. Also, solutions to the undampened forced problem have unbounded displacements when the driving frequency matches a natural frequency .
.Stress
Besides deflection, the beam equation describes forces and moments and can thus be used to describe stresses. For this reason, the Euler–Bernoulli beam equation is widely used in engineering, especially civil and mechanical, to determine the strength (as well as deflection) of beams under bending.
Both the bending moment and the shear force cause stresses in the beam. The stress due to shear force is maximum along the neutral axis of the beam (when the width of the beam, t, is constant along the cross section of the beam; otherwise an integral involving the first moment and the beam's width needs to be evaluated for the particular cross section), and the maximum tensile stress is at either the top or bottom surfaces. Thus the maximum principal stress in the beam may be neither at the surface nor at the center but in some general area. However, shear force stresses are negligible in comparison to bending moment stresses in all but the stockiest of beams as well as the fact that stress concentrations commonly occur at surfaces, meaning that the maximum stress in a beam is likely to be at the surface.
Simple or symmetrical bending
For beam cross-sections that are symmetrical about a plane perpendicular to the neutral plane, it can be shown that the tensile stress experienced by the beam may be expressed as:

 is the distance from the neutral axis to a point of interest; and
is the distance from the neutral axis to a point of interest; and is the bending moment. Note that this equation implies thatpure bending(of positive sign) will cause zero stress at the neutral axis, positive (tensile) stress at the "top" of the beam, and negative (compressive) stress at the bottom of the beam; and also implies that the maximum stress will be at the top surface and the minimum at the bottom. This bending stress may be superimposed with axially applied stresses, which will cause a shift in the neutral (zero stress) axis.
is the bending moment. Note that this equation implies thatpure bending(of positive sign) will cause zero stress at the neutral axis, positive (tensile) stress at the "top" of the beam, and negative (compressive) stress at the bottom of the beam; and also implies that the maximum stress will be at the top surface and the minimum at the bottom. This bending stress may be superimposed with axially applied stresses, which will cause a shift in the neutral (zero stress) axis.Maximum stresses at a cross-section
 and the maximum compressive stress is at the location
and the maximum compressive stress is at the location where the height of the cross-section is
where the height of the cross-section is . These stresses are
. These stresses are

 and we have one section modulus
and we have one section modulus .
.Strain in an Euler–Bernoulli beam
 (see Figure 1) and that the neutral surface does not change in length during the deformation.[6]
(see Figure 1) and that the neutral surface does not change in length during the deformation.[6] be the length of an element of the neutral surface in the undeformed state. For small deflections, the element does not change its length after bending but deforms into an arc of a circle of radius
be the length of an element of the neutral surface in the undeformed state. For small deflections, the element does not change its length after bending but deforms into an arc of a circle of radius . If
. If is the angle subtended by this arc, then
is the angle subtended by this arc, then .
. above the neutral surface. The initial length of this element is
above the neutral surface. The initial length of this element is . However, after bending, the length of the element becomes
. However, after bending, the length of the element becomes . The strain in that segment of the beam is given by
. The strain in that segment of the beam is given by
 is thecurvatureof the beam. This gives us the axial strain in the beam as a function of distance from the neutral surface. However, we still need to find a relation between the radius of curvature and the beam deflection
is thecurvatureof the beam. This gives us the axial strain in the beam as a function of distance from the neutral surface. However, we still need to find a relation between the radius of curvature and the beam deflection .
.Relation between curvature and beam deflection
 from the origin of the
from the origin of the coordinate system. The slope of the beam is approximately equal to the angle made by the neutral surface with the
coordinate system. The slope of the beam is approximately equal to the angle made by the neutral surface with the -axis for the small angles encountered in beam theory. Therefore, with this approximation,
-axis for the small angles encountered in beam theory. Therefore, with this approximation,
 , the relation
, the relation can be written as
can be written as
Hence the strain in the beam may be expressed as

Stress-strain relations
 , where
, where is theYoung's modulus. Hence the stress in an Euler–Bernoulli beam is given by
is theYoung's modulus. Hence the stress in an Euler–Bernoulli beam is given by
Note that the above relation, when compared with the relation between the axial stress and the bending moment, leads to

 , we also have
, we also have
Boundary considerations
 . To find a unique solution
. To find a unique solution we need four boundary conditions. The boundary conditions usually model supports, but they can also model point loads, distributed loads and moments. The support or displacement boundary conditions are used to fix values of displacement (
we need four boundary conditions. The boundary conditions usually model supports, but they can also model point loads, distributed loads and moments. The support or displacement boundary conditions are used to fix values of displacement ( ) and rotations (
) and rotations ( ) on the boundary. Such boundary conditions are also calledDirichlet boundary conditions. Load and moment boundary conditions involve higher derivatives of
) on the boundary. Such boundary conditions are also calledDirichlet boundary conditions. Load and moment boundary conditions involve higher derivatives of and representmomentum flux. Flux boundary conditions are also calledNeumann boundary conditions.
and representmomentum flux. Flux boundary conditions are also calledNeumann boundary conditions.As an example consider a cantilever beam that is built-in at one end and free at the other as shown in the adjacent figure. At the built-in end of the beam there cannot be any displacement or rotation of the beam. This means that at the left end both deflection and slope are zero. Since no external bending moment is applied at the free end of the beam, the bending moment at that location is zero. In addition, if there is no external force applied to the beam, the shear force at the free end is also zero.
 coordinate of the left end as
coordinate of the left end as and the right end as
and the right end as (the length of the beam), these statements translate to the following set of boundary conditions (assume
(the length of the beam), these statements translate to the following set of boundary conditions (assume is a constant):
is a constant):

 where F is the magnitude of a point force, and
where F is the magnitude of a point force, and where M is the magnitude of a point torque, the boundary conditions appropriate for some common cases is given in the table below. The change in a particular derivative of w across the boundary as x increases is denoted by
where M is the magnitude of a point torque, the boundary conditions appropriate for some common cases is given in the table below. The change in a particular derivative of w across the boundary as x increases is denoted by followed by that derivative. For example,
followed by that derivative. For example, where
where is the value of
is the value of at the lower boundary of the upper segment, while
at the lower boundary of the upper segment, while is the value of
is the value of at the upper boundary of the lower segment. When the values of the particular derivative are not only continuous across the boundary, but fixed as well, the boundary condition is written e.g.,
at the upper boundary of the lower segment. When the values of the particular derivative are not only continuous across the boundary, but fixed as well, the boundary condition is written e.g., which actually constitutes two separate equations (e.g.,
which actually constitutes two separate equations (e.g., = fixed).
= fixed).| Boundary |  |  |  |  |
|---|---|---|---|---|
| Clamp |  |  | ||
| Simple support |  |  |  | |
| Point force |  |  |  |  |
| Point torque |  |  |  |  |
| Free end |  |  | ||
| Clamp at end |  fixed fixed |  fixed fixed | ||
| Simply supported end |  |  fixed fixed | ||
| Point force at end |  |  | ||
| Point torque at end |  |  |
Note that in the first cases, in which the point forces and torques are located between two segments, there are four boundary conditions, two for the lower segment, and two for the upper. When forces and torques are applied to one end of the beam, there are two boundary conditions given which apply at that end. The sign of the point forces and torques at an end will be positive for the lower end, negative for the upper end.
Loading considerations
 which represents an external distributed load. Using distributed loading is often favorable for simplicity. Boundary conditions are, however, often used to model loads depending on context; this practice being especially common in vibration analysis.
which represents an external distributed load. Using distributed loading is often favorable for simplicity. Boundary conditions are, however, often used to model loads depending on context; this practice being especially common in vibration analysis. with an upward point load
with an upward point load applied at the free end. Using boundary conditions, this may be modeled in two ways. In the first approach, the applied point load is approximated by a shear force applied at the free end. In that case the governing equation and boundary conditions are:
applied at the free end. Using boundary conditions, this may be modeled in two ways. In the first approach, the applied point load is approximated by a shear force applied at the free end. In that case the governing equation and boundary conditions are:
Alternatively we can represent the point load as a distribution using the Dirac function. In that case the equation and boundary conditions are

Note that shear force boundary condition (third derivative) is removed, otherwise there would be a contradiction. These are equivalent boundary value problems, and both yield the solution

 being a piecewise function. Use of the Dirac function greatly simplifies such situations; otherwise the beam would have to be divided into sections, each with four boundary conditions solved separately. A well organized family of functions calledSingularity functionsare often used as a shorthand for the Dirac function, itsderivative, and itsantiderivatives.
being a piecewise function. Use of the Dirac function greatly simplifies such situations; otherwise the beam would have to be divided into sections, each with four boundary conditions solved separately. A well organized family of functions calledSingularity functionsare often used as a shorthand for the Dirac function, itsderivative, and itsantiderivatives.Dynamic phenomena can also be modeled using the static beam equation by choosing appropriate forms of the load distribution. As an example, the free vibration of a beam can be accounted for by using the load function:

 is thelinear mass densityof the beam, not necessarily a constant. With this time-dependent loading, the beam equation will be apartial differential equation:
is thelinear mass densityof the beam, not necessarily a constant. With this time-dependent loading, the beam equation will be apartial differential equation:
 :
:
 is a function of the displacement (the dependent variable), and the beam equation will be an autonomousordinary differential equation.
is a function of the displacement (the dependent variable), and the beam equation will be an autonomousordinary differential equation.Examples
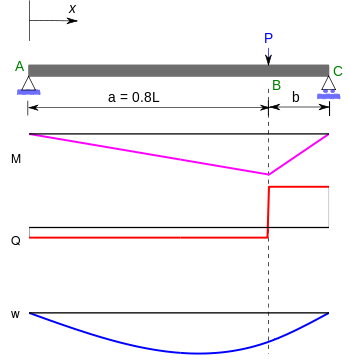
Three-point bending
 ), shear forces (
), shear forces ( ), and deflections (
), and deflections ( ) for a beam subjected to a central point load and an asymmetric point load are given in the table below.[6]
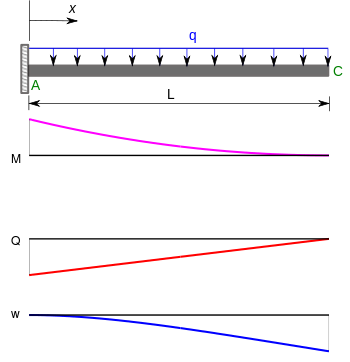
) for a beam subjected to a central point load and an asymmetric point load are given in the table below.[6]Cantilever beams
 ), shear forces (
), shear forces ( ), and deflections (
), and deflections ( ) for a cantilever beam subjected to a point load at the free end and a uniformly distributed load are given in the table below.[6]
) for a cantilever beam subjected to a point load at the free end and a uniformly distributed load are given in the table below.[6]Solutions for several other commonly encountered configurations are readily available in textbooks on mechanics of materials and engineering handbooks.
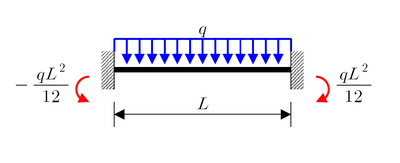
Statically indeterminate beams
The bending moments and shear forces in Euler–Bernoulli beams can often be determined directly using static balance of forces and moments. However, for certain boundary conditions, the number of reactions can exceed the number of independent equilibrium equations.[6] Such beams are called statically indeterminate.
The built-in beams shown in the figure below are statically indeterminate. To determine the stresses and deflections of such beams, the most direct method is to solve the Euler–Bernoulli beam equation with appropriate boundary conditions. But direct analytical solutions of the beam equation are possible only for the simplest cases. Therefore, additional techniques such as linear superposition are often used to solve statically indeterminate beam problems.
The superposition method involves adding the solutions of a number of statically determinate problems which are chosen such that the boundary conditions for the sum of the individual problems add up to those of the original problem.
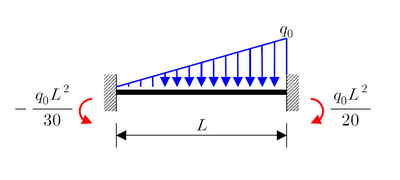
Another commonly encountered statically indeterminate beam problem is the cantilevered beam with the free end supported on a roller.[6] The bending moments, shear forces, and deflections of such a beam are listed below:
Extensions
The kinematic assumptions upon which the Euler–Bernoulli beam theory is founded allow it to be extended to more advanced analysis. Simple superposition allows for three-dimensional transverse loading. Using alternative constitutive equations can allow for viscoelastic or plastic beam deformation. Euler–Bernoulli beam theory can also be extended to the analysis of curved beams, beam buckling, composite beams, and geometrically nonlinear beam deflection.
Euler–Bernoulli beam theory does not account for the effects of transverse shear strain. As a result, it underpredicts deflections and overpredicts natural frequencies. For thin beams (beam length to thickness ratios of the order 20 or more) these effects are of minor importance. For thick beams, however, these effects can be significant. More advanced beam theories such as the Timoshenko beam theory (developed by the Russian-born scientist Stephen Timoshenko) have been developed to account for these effects.
Large deflections
The original Euler–Bernoulli theory is valid only for infinitesimal strains and small rotations. The theory can be extended in a straightforward manner to problems involving moderately large rotations provided that the strain remains small by using the von Kármán strains.[8]
The Euler–Bernoulli hypotheses that plane sections remain plane and normal to the axis of the beam lead to displacements of the form

Using the definition of the Lagrangian Green strain from finite strain theory, we can find the von Karman strains for the beam that are valid for large rotations but small strains. These strains have the form
![{\displaystyle {\begin{aligned}\varepsilon _{11}&={\cfrac {\mathrm {d} u_{0}}{dx_{1}}}-x_{3}{\cfrac {\mathrm {d} ^{2}w_{0}}{\mathrm {d} x_{1}^{2}}}+{\frac {1}{2}}\left[\left({\cfrac {\mathrm {d} u_{0}}{\mathrm {d} x_{1}}}-x_{3}{\cfrac {\mathrm {d} ^{2}w_{0}}{\mathrm {d} x_{1}^{2}}}\right)^{2}+\left({\cfrac {\mathrm {d} w_{0}}{\mathrm {d} x_{1}}}\right)^{2}\right]\\\varepsilon _{22}&=0\\\varepsilon _{33}&={\frac {1}{2}}\left({\cfrac {\mathrm {d} w_{0}}{\mathrm {d} x_{1}}}\right)^{2}\\\varepsilon _{23}&=0\\\varepsilon _{31}&={\frac {1}{2}}\left({\cfrac {\mathrm {d} w_{0}}{\mathrm {d} x_{1}}}-{\cfrac {\mathrm {d} w_{0}}{\mathrm {d} x_{1}}}\right)-{\frac {1}{2}}\left[\left({\cfrac {\mathrm {d} u_{0}}{\mathrm {d} x_{1}}}-x_{3}{\cfrac {\mathrm {d} ^{2}w_{0}}{\mathrm {d} x_{1}^{2}}}\right)\left({\cfrac {\mathrm {d} w_{0}}{\mathrm {d} x_{1}}}\right)\right]\\\varepsilon _{12}&=0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5df3e3a3b9f463577c57ef00d51bb095d92d8228)
From the principle of virtual work, the balance of forces and moments in the beams gives us the equilibrium equations

 is the axial load,
is the axial load, is the transverse load, and
is the transverse load, and
To close the system of equations we need the constitutive equations that relate stresses to strains (and hence stresses to displacements). For large rotations and small strains these relations are
![{\displaystyle {\begin{aligned}N_{xx}&=A_{xx}\left[{\cfrac {\mathrm {d} u_{0}}{dx}}+{\frac {1}{2}}\left({\cfrac {\mathrm {d} w_{0}}{\mathrm {d} x}}\right)^{2}\right]-B_{xx}{\cfrac {\mathrm {d} ^{2}w_{0}}{\mathrm {d} x^{2}}}\\M_{xx}&=B_{xx}\left[{\cfrac {du_{0}}{\mathrm {d} x}}+{\frac {1}{2}}\left({\cfrac {\mathrm {d} w_{0}}{\mathrm {d} x}}\right)^{2}\right]-D_{xx}{\cfrac {\mathrm {d} ^{2}w_{0}}{\mathrm {d} x^{2}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/56bebcb22431d51fea48f491324c3376ad94c6bf)
where

 is the *extensional stiffness*,
is the *extensional stiffness*, is the coupled extensional-bending stiffness, and
is the coupled extensional-bending stiffness, and is the *bending stiffness*.
is the *bending stiffness*.For the situation where the beam has a uniform cross-section and no axial load, the governing equation for a large-rotation Euler–Bernoulli beam is
See also
Applied mechanics
Bending
Bending moment
Buckling
Flexural rigidity
Generalised beam theory
Plate theory
Sandwich theory
Shear and moment diagram
Singularity function
Strain (materials science)
Timoshenko beam theory
Theorem of three moments (Clapeyron's theorem)
Three point flexural test



































![{\displaystyle M_{\mathrm {max} }={\cfrac {qL^{2}}{300}}[3{\sqrt {30}}-10]~;~~w_{\mathrm {max} }={\cfrac {qL^{4}}{2500EI}}[75-7{\sqrt {105}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c645a45da08a7383e7f7cfccc1fe79f26642657)








