Deductive reasoning
Deductive reasoning

Deductive reasoning, also deductive logic, is the process of reasoning from one or more statements (premises) to reach a logically certain conclusion.[1]
Deductive reasoning goes in the same direction as that of the conditionals, and links premises with conclusions. If all premises are true, the terms are clear, and the rules of deductive logic are followed, then the conclusion reached is necessarily true.
Deductive reasoning ("top-down logic") contrasts with inductive reasoning ("bottom-up logic") in the following way; in deductive reasoning, a conclusion is reached reductively by applying general rules which hold over the entirety of a closed domain of discourse, narrowing the range under consideration until only the conclusion(s) is left. In inductive reasoning, the conclusion is reached by generalizing or extra expolating from specific cases to general rules, i.e., there is epistemic uncertainty. However, the inductive reasoning mentioned here is not the same as induction used in mathematical proofs – mathematical induction is actually a form of deductive reasoning.
Deductive reasoning differs from abductive reasoning by the direction of the reasoning relative to the conditionals. Deductive reasoning goes in the same direction as that of the conditionals, whereas abductive reasoning goes in the opposite direction to that of the conditionals.
Simple example
An example of an argument using deductive reasoning:
All men are mortal.
(First premise)
Socrates is a man.
(Second premise)
Therefore, Socrates is mortal.
(Conclusion)
The first premise states that all objects classified as "men" have the attribute "mortal."
The second premise states that "Socrates" is classified as a "man" – a member of the set "men."
The conclusion then states that "Socrates" must be "mortal" because he inherits this attribute from his classification as a "man."
Reasoning with modus ponens, modus tollens, and the law of syllogism
Modus ponens
(First premise is a conditional statement)
(Second premise is the antecedent)
(Conclusion deduced is the consequent)
The following is an example of an argument using modus ponens:
If an angle satisfies 90° < < 180°, then is an obtuse angle.
= 120°.
is an obtuse angle.
Modus tollens
.
(First premise is a conditional statement)
.
(Second premise is the negation of the consequent)
.
(Conclusion deduced is the negation of the antecedent)
The following is an example of an argument using modus tollens:
If it is raining, then there are clouds in the sky.
There are no clouds in the sky.
Thus, it is not raining.
Law of syllogism
In proposition logic the syllogism
Therefore,.
The following is an example:
If the animal is a Yorkie, then it's a dog.
If the animal is a dog, then it's a mammal.
Therefore, if the animal is a Yorkie, then it's a mammal.
We deduced the final statement by combining the hypothesis of the first statement with the conclusion of the second statement.
We also allow that this could be a false statement.
This is an example of the transitive property in mathematics.
Another example is the transitive property of equality which can be stated in this form:
.
.
Therefore,.
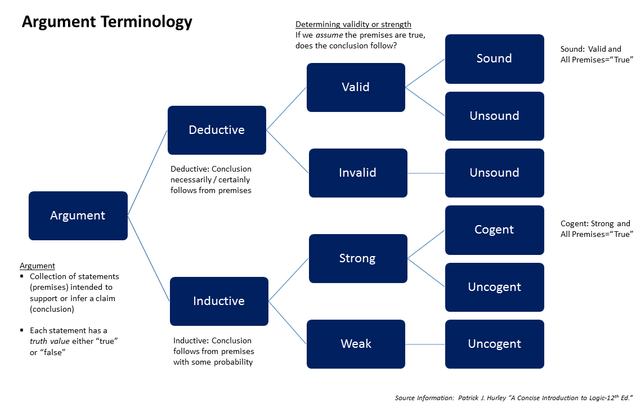
Validity and soundness
Deductive arguments are evaluated in terms of their validity and soundness
An argument is “valid” if it is impossible for its premises to be true while its conclusion is false. In other words, the conclusion must be true if the premises are true. An argument can be “valid” even if one or more of its premises are false.
An argument is “sound” if it is valid and the premises are true.
It is possible to have a deductive argument that is logically valid but is not sound. Fallacious arguments often take that form.
The following is an example of an argument that is “valid”, but not “sound”:
Everyone who eats carrots is a quarterback.
John eats carrots.
Therefore, John is a quarterback.
The example's first premise is false – there are people who eat carrots who are not quarterbacks – but the conclusion would necessarily be true, if the premises were true.
In other words, it is impossible for the premises to be true and the conclusion false.
Therefore, the argument is “valid”, but not “sound”.
False generalizations – such as "Everyone who eats carrots is a quarterback" – are often used to make unsound arguments.
The fact that there are some people who eat carrots but are not quarterbacks proves the flaw of the argument.
In this example, the first statement uses categorical reasoning, saying that all carrot-eaters are definitely quarterbacks. This theory of deductive reasoning – also known as term logic – was developed by Aristotle, but was superseded by propositional (sentential) logic and predicate logic.
Deductive reasoning can be contrasted with inductive reasoning, in regards to validity and soundness. In cases of inductive reasoning, even though the premises are true and the argument is “valid”, it is possible for the conclusion to be false (determined to be false with a counterexample or other means).
History
See also
Analogical reasoning
Argument (logic)
Argumentation theory
Correspondence theory of truth
Decision making
Decision theory
Defeasible reasoning
Fallacy
Fault Tree Analysis
Geometry
Hypothetico-deductive method
Inference
Inquiry
Legal syllogism
Logic and rationality
Logical consequence
Logical reasoning
Mathematical logic
Natural deduction
Peirce's theory of deductive reasoning
Propositional calculus
Retroductive reasoning
Subjective logic
Theory of justification