Bernoulli's principle
Bernoulli's principle


Video of a venturi meter used in a lab experiment
In fluid dynamics, Bernoulli's principle states that an increase in the speed of a fluid occurs simultaneously with a decrease in pressure or a decrease in the fluid's potential energy.[5] [] [6] [] The principle is named after Daniel Bernoulli who published it in his book Hydrodynamica in 1738.[7] Although Bernoulli deduced that pressure decreases when the flow speed increases, it was Leonhard Euler who derived Bernoulli's equation in its usual form in 1752.[8][9] The principle is only applicable for isentropic flows: when the effects of irreversible processes (like turbulence) and non-adiabatic processes (e.g. heat radiation) are small and can be neglected.
Bernoulli's principle can be applied to various types of fluid flow, resulting in various forms of Bernoulli's equation; there are different forms of Bernoulli's equation for different types of flow. The simple form of Bernoulli's equation is valid for incompressible flows (e.g. most liquid flows and gases moving at low Mach number). More advanced forms may be applied to compressible flows at higher Mach numbers (see the derivations of the Bernoulli equation).
Bernoulli's principle can be derived from the principle of conservation of energy. This states that, in a steady flow, the sum of all forms of energy in a fluid along a streamline is the same at all points on that streamline. This requires that the sum of kinetic energy, potential energy and internal energy remains constant.[6] [] Thus an increase in the speed of the fluid – implying an increase in its kinetic energy (dynamic pressure) – occurs with a simultaneous decrease in (the sum of) its potential energy (including the static pressure) and internal energy. If the fluid is flowing out of a reservoir, the sum of all forms of energy is the same on all streamlines because in a reservoir the energy per unit volume (the sum of pressure and gravitational potential ρ g h) is the same everywhere.[10] []
Bernoulli's principle can also be derived directly from Isaac Newton's Second Law of Motion. If a small volume of fluid is flowing horizontally from a region of high pressure to a region of low pressure, then there is more pressure behind than in front. This gives a net force on the volume, accelerating it along the streamline.[1][2][3]
Fluid particles are subject only to pressure and their own weight. If a fluid is flowing horizontally and along a section of a streamline, where the speed increases it can only be because the fluid on that section has moved from a region of higher pressure to a region of lower pressure; and if its speed decreases, it can only be because it has moved from a region of lower pressure to a region of higher pressure. Consequently, within a fluid flowing horizontally, the highest speed occurs where the pressure is lowest, and the lowest speed occurs where the pressure is highest.[14]
Incompressible flow equation
In most flows of liquids, and of gases at low Mach number, the density of a fluid parcel can be considered to be constant, regardless of pressure variations in the flow. Therefore, the fluid can be considered to be incompressible and these flows are called incompressible flows. Bernoulli performed his experiments on liquids, so his equation in its original form is valid only for incompressible flow. A common form of Bernoulli's equation, valid at any arbitrary point along a streamline, is:
 | **(A)** |
where:
- vis the fluid flowspeedat a point on a streamline,gis theacceleration due to gravity,zis theelevationof the point above a reference plane, with the positivez-direction pointing upward – so in the direction opposite to the gravitational acceleration,pis thepressureat the chosen point, andρis thedensityof the fluid at all points in the fluid.
The constant on the right-hand side of the equation depends only on the streamline chosen, whereas v, z and p depend on the particular point on that streamline.

where Ψ is the force potential at the point considered on the streamline. E.g. for the Earth's gravity Ψ = gz.
By multiplying with the fluid density ρ, equation (A) can be rewritten as:

or:

where
The constant in the Bernoulli equation can be normalised. A common approach is in terms of total head or energy head H:

The above equations suggest there is a flow speed at which pressure is zero, and at even higher speeds the pressure is negative. Most often, gases and liquids are not capable of negative absolute pressure, or even zero pressure, so clearly Bernoulli's equation ceases to be valid before zero pressure is reached. In liquids – when the pressure becomes too low – cavitation occurs. The above equations use a linear relationship between flow speed squared and pressure. At higher flow speeds in gases, or for sound waves in liquid, the changes in mass density become significant so that the assumption of constant density is invalid.
Simplified form
In many applications of Bernoulli's equation, the change in the ρgz term along the streamline is so small compared with the other terms that it can be ignored. For example, in the case of aircraft in flight, the change in height z along a streamline is so small the ρgz term can be omitted. This allows the above equation to be presented in the following simplified form:

where p0 is called "total pressure", and q is "dynamic pressure".[18] Many authors refer to the pressure p as static pressure to distinguish it from total pressure p0 and dynamic pressure q. In Aerodynamics, L.J. Clancy writes: "To distinguish it from the total and dynamic pressures, the actual pressure of the fluid, which is associated not with its motion but with its state, is often referred to as the static pressure, but where the term pressure alone is used it refers to this static pressure."[5] []
- static pressure + dynamic pressure = total pressure
Every point in a steadily flowing fluid, regardless of the fluid speed at that point, has its own unique static pressure p and dynamic pressure q. Their sum p + q is defined to be the total pressure p0. The significance of Bernoulli's principle can now be summarized as "total pressure is constant along a streamline".
If the fluid flow is irrotational, the total pressure on every streamline is the same and Bernoulli's principle can be summarized as "total pressure is constant everywhere in the fluid flow".[5] [] It is reasonable to assume that irrotational flow exists in any situation where a large body of fluid is flowing past a solid body. Examples are aircraft in flight, and ships moving in open bodies of water. However, it is important to remember that Bernoulli's principle does not apply in the boundary layer or in fluid flow through long pipes.
If the fluid flow at some point along a streamline is brought to rest, this point is called a stagnation point, and at this point the total pressure is equal to the stagnation pressure.
Applicability of incompressible flow equation to flow of gases
Bernoulli's equation is sometimes valid for the flow of gases: provided that there is no transfer of kinetic or potential energy from the gas flow to the compression or expansion of the gas. If both the gas pressure and volume change simultaneously, then work will be done on or by the gas. In this case, Bernoulli's equation – in its incompressible flow form – cannot be assumed to be valid. However, if the gas process is entirely isobaric, or isochoric, then no work is done on or by the gas, (so the simple energy balance is not upset). According to the gas law, an isobaric or isochoric process is ordinarily the only way to ensure constant density in a gas. Also the gas density will be proportional to the ratio of pressure and absolute temperature, however this ratio will vary upon compression or expansion, no matter what non-zero quantity of heat is added or removed. The only exception is if the net heat transfer is zero, as in a complete thermodynamic cycle, or in an individual isentropic (frictionless adiabatic) process, and even then this reversible process must be reversed, to restore the gas to the original pressure and specific volume, and thus density. Only then is the original, unmodified Bernoulli equation applicable. In this case the equation can be used if the flow speed of the gas is sufficiently below the speed of sound, such that the variation in density of the gas (due to this effect) along each streamline can be ignored. Adiabatic flow at less than Mach 0.3 is generally considered to be slow enough.
Unsteady potential flow
The Bernoulli equation for unsteady potential flow is used in the theory of ocean surface waves and acoustics.

which is a Bernoulli equation valid also for unsteady—or time dependent—flows. Here ∂φ/∂t denotes the partial derivative of the velocity potential φ with respect to time t, and v = |∇φ| is the flow speed. The function f(t) depends only on time and not on position in the fluid. As a result, the Bernoulli equation at some moment t does not only apply along a certain streamline, but in the whole fluid domain. This is also true for the special case of a steady irrotational flow, in which case f and ∂φ/∂t are constants so equation (A) can be applied in every point of the fluid domain.[6] []
Further f(t) can be made equal to zero by incorporating it into the velocity potential using the transformation

resulting in

Note that the relation of the potential to the flow velocity is unaffected by this transformation: ∇Φ = ∇φ.
The Bernoulli equation for unsteady potential flow also appears to play a central role in Luke's variational principle, a variational description of free-surface flows using the Lagrangian (not to be confused with Lagrangian coordinates).
Compressible flow equation
Bernoulli developed his principle from his observations on liquids, and his equation is applicable only to incompressible fluids, and steady compressible fluids up to approximately Mach number 0.3.[19] It is possible to use the fundamental principles of physics to develop similar equations applicable to compressible fluids. There are numerous equations, each tailored for a particular application, but all are analogous to Bernoulli's equation and all rely on nothing more than the fundamental principles of physics such as Newton's laws of motion or the first law of thermodynamics.
Compressible flow in fluid dynamics
For a compressible fluid, with a barotropic equation of state, and under the action of conservative forces,[20]

where:

where, in addition to the terms listed above:
γ is the ratio of the specific heats of the fluid
g is the acceleration due to gravity
z is the elevation of the point above a reference plane
In many applications of compressible flow, changes in elevation are negligible compared to the other terms, so the term gz can be omitted. A very useful form of the equation is then:

where:
p0 is the total pressure
ρ0 is the total density
Compressible flow in thermodynamics

Here w is the enthalpy per unit mass (also known as specific enthalpy), which is also often written as h (not to be confused with "head" or "height").
Note that w = ε + p/ρ where ε is the thermodynamic energy per unit mass, also known as the specific internal energy. So, for constant internal energy ε the equation reduces to the incompressible-flow form.
The constant on the right-hand side is often called the Bernoulli constant, and denoted b. For steady inviscid adiabatic flow with no additional sources or sinks of energy, b is constant along any given streamline. More generally, when b may vary along streamlines, it still proves a useful parameter, related to the "head" of the fluid (see below).
When the change in Ψ can be ignored, a very useful form of this equation is:

where w0 is total enthalpy. For a calorically perfect gas such as an ideal gas, the enthalpy is directly proportional to the temperature, and this leads to the concept of the total (or stagnation) temperature.
When shock waves are present, in a reference frame in which the shock is stationary and the flow is steady, many of the parameters in the Bernoulli equation suffer abrupt changes in passing through the shock. The Bernoulli parameter itself, however, remains unaffected. An exception to this rule is radiative shocks, which violate the assumptions leading to the Bernoulli equation, namely the lack of additional sinks or sources of energy.
Derivations of the Bernoulli equation
- Derivation through integrating Newton's Second Law of Motion
- Derivation by using conservation of energy
- the change in the kinetic energyEkin*of the system equals the net workWdone on the system*;
- *theworkdone by theforcesin the fluid equals increase inkinetic energy.*
- The work done by the pressure acting on the areasA1andA2
- The work done by gravity: the gravitational potential energy in the volumeA1s1is lost, and at the outflow in the volumeA2s2is gained. So, the change in gravitational potential energyΔEpot,gravityin the time intervalΔtis
- Now, thework by the force of gravity is opposite to the change in potential energy,Wgravity= −ΔEpot,gravity: while the force of gravity is in the negativez-direction, the work—gravity force times change in elevation—will be negative for a positive elevation changeΔz = z2− z1, while the corresponding potential energy change is positive.[25](§14–3)So:
(Eqn. 1), Which is also Equation (A)
(Eqn. 2a)
(Eqn. 2b)
(Eqn. 3)
| Bernoulli equation for incompressible fluids |
|---|
| The Bernoulli equation for incompressible fluids can be derived by eitherintegratingNewton's second law of motionor by applying the law ofconservation of energybetween two sections along a streamline, ignoringviscosity, compressibility, and thermal effects. |
.
| Bernoulli equation for compressible fluids |
|---|
| The derivation for compressible fluids is similar. Again, the derivation depends upon (1) conservation of mass, and (2) conservation of energy. Conservation of mass implies that in the above figure, in the interval of timeΔt, the amount of mass passing through the boundary defined by the areaA1is equal to the amount of mass passing outwards through the boundary defined by the areaA2: |
Applications

Condensation visible over the upper surface of an Airbus A340 wing caused by the fall in temperature accompanying the fall in pressure.
In modern everyday life there are many observations that can be successfully explained by application of Bernoulli's principle, even though no real fluid is entirely inviscid[26] and a small viscosity often has a large effect on the flow.
Bernoulli's principle can be used to calculate the lift force on an airfoil, if the behaviour of the fluid flow in the vicinity of the foil is known. For example, if the air flowing past the top surface of an aircraft wing is moving faster than the air flowing past the bottom surface, then Bernoulli's principle implies that the pressure on the surfaces of the wing will be lower above than below. This pressure difference results in an upwards lifting force.[4][27] Whenever the distribution of speed past the top and bottom surfaces of a wing is known, the lift forces can be calculated (to a good approximation) using Bernoulli's equations[28] – established by Bernoulli over a century before the first man-made wings were used for the purpose of flight. Bernoulli's principle does not explain why the air flows faster past the top of the wing and slower past the underside. See the article on aerodynamic lift for more info.
The carburettor used in many reciprocating engines contains a venturi to create a region of low pressure to draw fuel into the carburettor and mix it thoroughly with the incoming air. The low pressure in the throat of a venturi can be explained by Bernoulli's principle; in the narrow throat, the air is moving at its fastest speed and therefore it is at its lowest pressure.
An injector on a steam locomotive (or static boiler).
The pitot tube and static port on an aircraft are used to determine the airspeed of the aircraft. These two devices are connected to the airspeed indicator, which determines the dynamic pressure of the airflow past the aircraft. Dynamic pressure is the difference between stagnation pressure and static pressure. Bernoulli's principle is used to calibrate the airspeed indicator so that it displays the indicated airspeed appropriate to the dynamic pressure.[5] []
A De Laval nozzle utilizes Bernoulli's principle to create a force by turning pressure energy generated by the combustion of propellants into velocity. This then generates thrust by way of Newton's third law of motion.
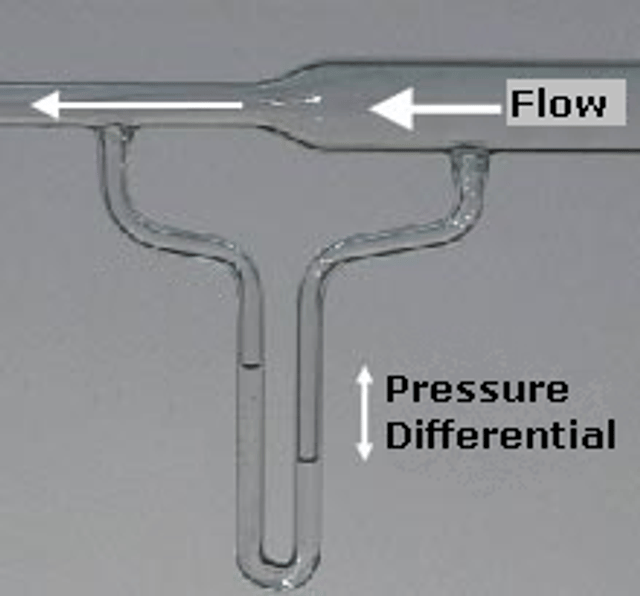
The flow speed of a fluid can be measured using a device such as a Venturi meter or an orifice plate, which can be placed into a pipeline to reduce the diameter of the flow. For a horizontal device, the continuity equation shows that for an incompressible fluid, the reduction in diameter will cause an increase in the fluid flow speed. Subsequently, Bernoulli's principle then shows that there must be a decrease in the pressure in the reduced diameter region. This phenomenon is known as the Venturi effect.
The maximum possible drain rate for a tank with a hole or tap at the base can be calculated directly from Bernoulli's equation, and is found to be proportional to the square root of the height of the fluid in the tank. This is Torricelli's law, showing that Torricelli's law is compatible with Bernoulli's principle. Viscosity lowers this drain rate. This is reflected in the discharge coefficient, which is a function of the Reynolds number and the shape of the orifice.[29]
The Bernoulli grip relies on this principle to create a non-contact adhesive force between a surface and the gripper.
Bernoulli's principle is also applicable in the swinging of a cricket ball. During a cricket match, bowlers continually polish one side of the ball. After some time, one side is quite rough and the other is still smooth. Hence, when the ball is bowled and passes through air, the speed on one side of the ball is faster than on the other, due to this difference in smoothness, and this results in a pressure difference between the sides; this leads to the ball rotating ("swinging") while travelling through the air, giving advantage to the bowlers.
Misunderstandings about the generation of lift
Many explanations for the generation of lift (on airfoils, propeller blades, etc.) can be found; some of these explanations can be misleading, and some are false.[30] There has been debate about whether lift is best introduced to students using Bernoulli's principle or Newton's laws of motion. Modern writings agree that both Bernoulli's principle and Newton's laws are relevant, and either can be used to correctly describe lift.[16][31][32]
Several of these explanations use the Bernoulli principle to connect the flow kinematics to the flow-induced pressures. In cases of incorrect (or partially correct) explanations relying on the Bernoulli principle, the errors generally occur in the assumptions on the flow kinematics and how these are produced. It is not the Bernoulli principle itself that is questioned, because this principle is well established (the airflow above the wing is faster, the question is why it is faster).[33][6] [] [34] [] [35]
Misapplications of Bernoulli's principle in common classroom demonstrations
There are several common classroom demonstrations that are sometimes incorrectly explained using Bernoulli's principle.[36] One involves holding a piece of paper horizontally so that it droops downward and then blowing over the top of it. As the demonstrator blows over the paper, the paper rises. It is then asserted that this is because "faster moving air has lower pressure".[37][38][39]
One problem with this explanation can be seen by blowing along the bottom of the paper: were the deflection due simply to faster moving air one would expect the paper to deflect downward, but the paper deflects upward regardless of whether the faster moving air is on the top or the bottom.[40] Another problem is that when the air leaves the demonstrator's mouth it has the same pressure as the surrounding air;[41] the air does not have lower pressure just because it is moving; in the demonstration, the static pressure of the air leaving the demonstrator's mouth is equal to the pressure of the surrounding air.[42][43] A third problem is that it is false to make a connection between the flow on the two sides of the paper using Bernoulli’s equation since the air above and below are different flow fields and Bernoulli's principle only applies within a flow field.[44][45][46][47]
As the wording of the principle can change its implications, stating the principle correctly is important.[48] What Bernoulli's principle actually says is that within a flow of constant energy, when fluid flows through a region of lower pressure it speeds up and vice versa.[49] Thus, Bernoulli's principle concerns itself with changes in speed and changes in pressure within a flow field. It cannot be used to compare different flow fields.
A correct explanation of why the paper rises would observe that the plume follows the curve of the paper and that a curved streamline will develop a pressure gradient perpendicular to the direction of flow, with the lower pressure on the inside of the curve.[50][51][52][53] Bernoulli's principle predicts that the decrease in pressure is associated with an increase in speed, i.e. that as the air passes over the paper it speeds up and moves faster than it was moving when it left the demonstrator's mouth. But this is not apparent from the demonstration.[54][55][56]
See also
Daniel Bernoulli
Coandă effect
Euler equations – for the flow of an inviscid fluid
Hydraulics – applied fluid mechanics for liquids
Navier–Stokes equations – for the flow of a viscous fluid
Terminology in fluid dynamics
Torricelli's law – a special case of Bernoulli's principle
























