Viscosity

Viscosity

| Viscosity | |
|---|---|
Common symbols | η,μ |
Derivations from other quantities | μ = G·t |
The viscosity of a fluid is a measure of its resistance to deformation at a given rate. For liquids, it corresponds to the informal concept of "thickness": for example, syrup has a higher viscosity than water.[3]
Viscosity can be conceptualized as quantifying the frictional force that arises between adjacent layers of fluid that are in relative motion. For instance, when a fluid is forced through a tube, it flows more quickly near the tube's axis than near its walls. In such a case, experiments show that some stress (such as a pressure difference between the two ends of the tube) is needed to sustain the flow through the tube. This is because a force is required to overcome the friction between the layers of the fluid which are in relative motion: the strength of this force is proportional to the viscosity.
A fluid that has no resistance to shear stress is known as an ideal or inviscid fluid. Zero viscosity is observed only at very low temperatures in superfluids. Otherwise, the second law of thermodynamics requires all fluids to have positive viscosity;[4][5] such fluids are technically said to be viscous or viscid. A fluid with a high viscosity, such as pitch, may appear to be a solid.
| Viscosity | |
|---|---|
Common symbols | η,μ |
Derivations from other quantities | μ = G·t |
Etymology
Definition
Simple definition

Illustration of a planar Couette flow. Since the shearing flow is opposed by friction between adjacent layers of fluid (which are in relative motion), a force is required to sustain the motion of the upper plate. The relative strength of this force is a measure of the fluid's viscosity.

In a general parallel flow, the shear stress is proportional to the gradient of the velocity.
In materials science and engineering, one is often interested in understanding the forces, or stresses, involved in the deformation of a material. For instance, if the material were a simple spring, the answer would be given by Hooke's law, which says that the force experienced by a spring is proportional to the distance displaced from equilibrium. Stresses which can be attributed to the deformation of a material from some rest state are called elastic stresses. In other materials, stresses are present which can be attributed to the rate of change of the deformation over time. These are called viscous stresses. For instance, in a fluid such as water the stresses which arise from shearing the fluid do not depend on the distance the fluid has been sheared; rather, they depend on how quickly the shearing occurs.
Viscosity is the material property which relates the viscous stresses in a material to the rate of change of a deformation (the strain rate). Although it applies to general flows, it is easy to visualize and define in a simple shearing flow, such as a planar Couette flow.
 (see illustration to the right). If the speed of the top plate is low enough (to avoid turbulence), then in steady state the fluid particles move parallel to it, and their speed varies from
(see illustration to the right). If the speed of the top plate is low enough (to avoid turbulence), then in steady state the fluid particles move parallel to it, and their speed varies from at the bottom to
at the bottom to at the top.[7] Each layer of fluid moves faster than the one just below it, and friction between them gives rise to aforceresisting their relative motion. In particular, the fluid applies on the top plate a force in the direction opposite to its motion, and an equal but opposite force on the bottom plate. An external force is therefore required in order to keep the top plate moving at constant speed.
at the top.[7] Each layer of fluid moves faster than the one just below it, and friction between them gives rise to aforceresisting their relative motion. In particular, the fluid applies on the top plate a force in the direction opposite to its motion, and an equal but opposite force on the bottom plate. An external force is therefore required in order to keep the top plate moving at constant speed. at the top. Moreover, the magnitude
at the top. Moreover, the magnitude of the force acting on the top plate is found to be proportional to the speed
of the force acting on the top plate is found to be proportional to the speed and the area
and the area of each plate, and inversely proportional to their separation
of each plate, and inversely proportional to their separation :
:
 is the viscosity of the fluid, with units of
is the viscosity of the fluid, with units of (pascal
(pascal is called the rate of shear deformation or *shear velocity*, and is thederivativeof the fluid speed in the directionperpendicularto the plates (see illustrations to the right). If the velocity does not vary linearly with
is called the rate of shear deformation or *shear velocity*, and is thederivativeof the fluid speed in the directionperpendicularto the plates (see illustrations to the right). If the velocity does not vary linearly with , then the appropriate generalization is
, then the appropriate generalization is
 , and
, and is the local shear velocity. This expression is referred to as Newton's law of viscosity. In shearing flows with planar symmetry, it is what defines
is the local shear velocity. This expression is referred to as Newton's law of viscosity. In shearing flows with planar symmetry, it is what defines . It is a special case of the general definition of viscosity (see below), which can be expressed in coordinate-free form.
. It is a special case of the general definition of viscosity (see below), which can be expressed in coordinate-free form. ) for the viscosity is common among mechanical and chemical engineers, as well as physicists.[8][9][10] However, theGreek letter eta(
) for the viscosity is common among mechanical and chemical engineers, as well as physicists.[8][9][10] However, theGreek letter eta( ) is also used by chemists, physicists, and theIUPAC.[11] The viscosity
) is also used by chemists, physicists, and theIUPAC.[11] The viscosity is sometimes also referred to as the shear viscosity. However, at least one author discourages the use of this terminology, noting that
is sometimes also referred to as the shear viscosity. However, at least one author discourages the use of this terminology, noting that can appear in nonshearing flows in addition to shearing flows.[12]
can appear in nonshearing flows in addition to shearing flows.[12]General definition
In very general terms, the viscous stresses in a fluid are defined as those resulting from the relative velocity of different fluid particles. As such, the viscous stresses must depend on spatial gradients of the flow velocity. If the velocity gradients are small, then to a first approximation the viscous stresses depend only on the first derivatives of the velocity.[13] (For Newtonian fluids, this is also a linear dependence.) In Cartesian coordinates, the general relationship can then be written as

 is a viscosity tensor that maps the strain rate tensor
is a viscosity tensor that maps the strain rate tensor onto the viscous stress tensor
onto the viscous stress tensor .[14] Since the indices in this expression can vary from 1 to 3, there are 81 "viscosity coefficients"
.[14] Since the indices in this expression can vary from 1 to 3, there are 81 "viscosity coefficients" in total. However, due to spatial symmetries these coefficients are not all independent. For instance, forisotropicNewtonian fluids, the 81 coefficients can be reduced to 2 independent parameters. The most usual decomposition yields the standard (scalar) viscosity
in total. However, due to spatial symmetries these coefficients are not all independent. For instance, forisotropicNewtonian fluids, the 81 coefficients can be reduced to 2 independent parameters. The most usual decomposition yields the standard (scalar) viscosity and thebulk viscosity
and thebulk viscosity :
:![{\displaystyle \mathbf {\tau } =\mu \left[\nabla \mathbf {v} +(\nabla \mathbf {v} )^{\dagger }\right]-\left({\frac {2}{3}}\mu -\kappa \right)(\nabla \cdot \mathbf {v} )\mathbf {\delta } ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a3d8d9a7b9d48854ded27cabf22577676ee9188)
 is frequently not necessary in fluid dynamics problems. For example, an incompressible fluid satisfies
is frequently not necessary in fluid dynamics problems. For example, an incompressible fluid satisfies and so the term containing
and so the term containing drops out. Moreover,
drops out. Moreover, is often assumed to be negligible for gases since it is
is often assumed to be negligible for gases since it is in amonoatomicideal gas.[12] One situation in which
in amonoatomicideal gas.[12] One situation in which can be important is the calculation of energy loss insoundandshock waves, described byStokes' law of sound attenuation, since these phenomena involve rapid expansions and compressions.
can be important is the calculation of energy loss insoundandshock waves, described byStokes' law of sound attenuation, since these phenomena involve rapid expansions and compressions.It is worth emphasizing that the above expressions are not fundamental laws of nature, but rather definitions of viscosity. As such, their utility for any given material, as well as means for measuring or calculating the viscosity, must be established using separate means.
Dynamic and kinematic viscosity
 :
: .
. is frequently called the dynamic viscosity or absolute viscosity, and has units force × time/area.
is frequently called the dynamic viscosity or absolute viscosity, and has units force × time/area.Momentum transport
 , the shear stress
, the shear stress has units equivalent to a momentumflux, i.e. momentum per unit time per unit area. Thus,
has units equivalent to a momentumflux, i.e. momentum per unit time per unit area. Thus, can be interpreted as specifying the flow of momentum in the
can be interpreted as specifying the flow of momentum in the direction from one fluid layer to the next. Per Newton's law of viscosity, this momentum flow occurs across a velocity gradient, and the magnitude of the corresponding momentum flux is determined by the viscosity.
direction from one fluid layer to the next. Per Newton's law of viscosity, this momentum flow occurs across a velocity gradient, and the magnitude of the corresponding momentum flux is determined by the viscosity.The analogy with heat and mass transfer can be made explicit. Just as heat flows from high temperature to low temperature and mass flows from high density to low density, momentum flows from high velocity to low velocity. These behaviors are all described by compact expressions, called constitutive relations, whose one-dimensional forms are given here:

 is the density,
is the density, and
and are the mass and heat fluxes, and
are the mass and heat fluxes, and and
and are the mass diffusivity and thermal conductivity.[17] The fact that mass, momentum, and energy (heat) transport are among the most relevant processes in continuum mechanics is not a coincidence: these are among the few physical quantities that are conserved at the microscopic level in interparticle collisions. Thus, rather than being dictated by the fast and complex microscopic interaction timescale, their dynamics occurs on macroscopic timescales, as described by the various equations of transport theory and hydrodynamics.
are the mass diffusivity and thermal conductivity.[17] The fact that mass, momentum, and energy (heat) transport are among the most relevant processes in continuum mechanics is not a coincidence: these are among the few physical quantities that are conserved at the microscopic level in interparticle collisions. Thus, rather than being dictated by the fast and complex microscopic interaction timescale, their dynamics occurs on macroscopic timescales, as described by the various equations of transport theory and hydrodynamics.Newtonian and non-Newtonian fluids
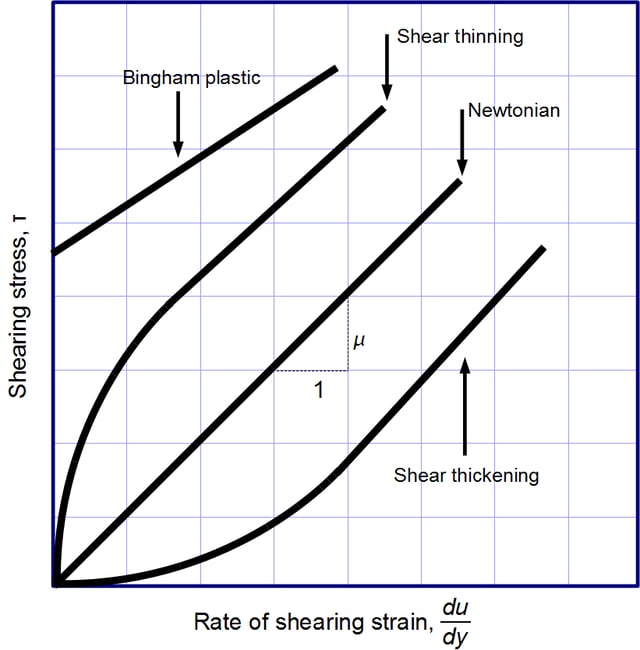
Viscosity, the slope of each line, varies among materials.
 . Its form is motivated by experiments which show that for a wide range of fluids,
. Its form is motivated by experiments which show that for a wide range of fluids, is independent of strain rate. Such fluids are calledNewtonian.Gases,water, and many common liquids can be considered Newtonian in ordinary conditions and contexts. However, there are manynon-Newtonian fluidsthat significantly deviate from this behavior. For example:
is independent of strain rate. Such fluids are calledNewtonian.Gases,water, and many common liquids can be considered Newtonian in ordinary conditions and contexts. However, there are manynon-Newtonian fluidsthat significantly deviate from this behavior. For example:Shear-thickening liquids, whose viscosity increases with the rate of shear strain.
Shear-thinning liquids, whose viscosity decreases with the rate of shear strain.
Thixotropic liquids, that become less viscous over time when shaken, agitated, or otherwise stressed.
Rheopectic (dilatant) liquids, that become more viscous over time when shaken, agitated, or otherwise stressed.
Bingham plastics that behave as a solid at low stresses but flow as a viscous fluid at high stresses.
Even for a Newtonian fluid, the viscosity usually depends on its composition and temperature. For gases and other compressible fluids, it depends on temperature and varies very slowly with pressure. The viscosity of some fluids may depend on other factors. A magnetorheological fluid, for example, becomes thicker when subjected to a magnetic field, possibly to the point of behaving like a solid.
In solids
The viscous forces that arise during fluid flow must not be confused with the elastic forces that arise in a solid in response to shear, compression or extension stresses. While in the latter the stress is proportional to the amount of shear deformation, in a fluid it is proportional to the rate of deformation over time. (For this reason, Maxwell used the term fugitive elasticity for fluid viscosity.)
However, many liquids (including water) will briefly react like elastic solids when subjected to sudden stress. Conversely, many "solids" (even granite) will flow like liquids, albeit very slowly, even under arbitrarily small stress.[21] Such materials are therefore best described as possessing both elasticity (reaction to deformation) and viscosity (reaction to rate of deformation); that is, being viscoelastic.
Indeed, some authors have claimed that amorphous solids, such as glass and many polymers, are actually liquids with a very high viscosity (greater than 1012 Pa·s).[22][23] However, other authors dispute this hypothesis, claiming instead that there is some threshold for the stress, below which most solids will not flow at all,[24] and that alleged instances of glass flow in window panes of old buildings are due to the crude manufacturing process of older eras rather than to the viscosity of glass.[25]
Viscoelastic solids may exhibit both shear viscosity and bulk viscosity. The extensional viscosity is a linear combination of the shear and bulk viscosities that describes the reaction of a solid elastic material to elongation. It is widely used for characterizing polymers.
Measurement
Viscosity is measured with various types of viscometers and rheometers. A rheometer is used for those fluids that cannot be defined by a single value of viscosity and therefore require more parameters to be set and measured than is the case for a viscometer. Close temperature control of the fluid is essential to acquire accurate measurements, particularly in materials like lubricants, whose viscosity can double with a change of only 5 °C.
For some fluids, the viscosity is constant over a wide range of shear rates (Newtonian fluids). The fluids without a constant viscosity (non-Newtonian fluids) cannot be described by a single number. Non-Newtonian fluids exhibit a variety of different correlations between shear stress and shear rate.
One of the most common instruments for measuring kinematic viscosity is the glass capillary viscometer.
In coating industries, viscosity may be measured with a cup in which the efflux time is measured. There are several sorts of cup – such as the Zahn cup and the Ford viscosity cup – with the usage of each type varying mainly according to the industry. The efflux time can also be converted to kinematic viscosities (centistokes, cSt) through the conversion equations.
Also used in coatings, a Stormer viscometer uses load-based rotation in order to determine viscosity. The viscosity is reported in Krebs units (KU), which are unique to Stormer viscometers.
Vibrating viscometers can also be used to measure viscosity. Resonant, or vibrational viscometers work by creating shear waves within the liquid. In this method, the sensor is submerged in the fluid and is made to resonate at a specific frequency. As the surface of the sensor shears through the liquid, energy is lost due to its viscosity. This dissipated energy is then measured and converted into a viscosity reading. A higher viscosity causes a greater loss of energy.
Extensional viscosity can be measured with various rheometers that apply extensional stress.
Volume viscosity can be measured with an acoustic rheometer.
Apparent viscosity is a calculation derived from tests performed on drilling fluid used in oil or gas well development. These calculations and tests help engineers develop and maintain the properties of the drilling fluid to the specifications required.
Units
The SI unit of dynamic viscosity is the pascal-second (Pa·s), or equivalently kilogram per meter per second (kg·m−1·s−1). The CGS unit is called the poise (P),[27] named after Jean Léonard Marie Poiseuille. It is commonly expressed, particularly in ASTM standards, as centipoise (cP) since the latter is equal to the SI multiple millipascal seconds (mPa·s).
The SI unit of kinematic viscosity is square meter per second (m2/s), whereas the CGS unit for kinematic viscosity is the stokes (St), named after Sir George Gabriel Stokes.[28] In U.S. usage, stoke is sometimes used as the singular form. The submultiple centistokes (cSt) is often used instead.
 or
or , depending on the convention used, measured in reciprocal poise (P−1, orcm·s·g−1), sometimes called the rhe. Fluidity is seldom used inengineeringpractice.
, depending on the convention used, measured in reciprocal poise (P−1, orcm·s·g−1), sometimes called the rhe. Fluidity is seldom used inengineeringpractice.Nonstandard units include the reyn, a British unit of dynamic viscosity. In the automotive industry the viscosity index is used to describe the change of viscosity with temperature.
At one time the petroleum industry relied on measuring kinematic viscosity by means of the Saybolt viscometer, and expressing kinematic viscosity in units of Saybolt universal seconds (SUS).[29] Other abbreviations such as SSU (Saybolt seconds universal) or SUV (Saybolt universal viscosity) are sometimes used. Kinematic viscosity in centistokes can be converted from SUS according to the arithmetic and the reference table provided in ASTM D 2161.
Molecular origins
In general, the viscosity of a system depends in detail on how the molecules constituting the system interact. There are no simple but correct expressions for the viscosity of a fluid. The simplest exact expressions are the Green–Kubo relations for the linear shear viscosity or the transient time correlation function expressions derived by Evans and Morriss in 1988.[30] Although these expressions are each exact, calculating the viscosity of a dense fluid using these relations currently requires the use of molecular dynamics computer simulations. On the other hand, much more progress can be made for a dilute gas. Even elementary assumptions about how gas molecules move and interact lead to a basic understanding of the molecular origins of viscosity. More sophisticated treatments can be constructed by systematically coarse-graining the equations of motion of the gas molecules. An example of such a treatment is Chapman–Enskog theory, which derives expressions for the viscosity of a dilute gas from the Boltzmann equation.[31]
Momentum transport in gases is generally mediated by discrete molecular collisions, and in liquids by attractive forces which bind molecules close together.[16] Because of this, the dynamic viscosities of liquids are typically much larger than those of gases.
Pure gases
,
| Elementary calculation of viscosity for a dilute gas |
|---|
Consider a dilute gas moving parallel to the -axis with velocity -axis with velocity that depends only on the that depends only on the coordinate. To simplify the discussion, the gas is assumed to have uniform temperature and density.
Under these assumptions, the coordinate. To simplify the discussion, the gas is assumed to have uniform temperature and density.
Under these assumptions, the velocity of a molecule passing through velocity of a molecule passing through is equal to whatever velocity that molecule had when its mean free path is equal to whatever velocity that molecule had when its mean free path began. Because began. Because is typically small compared with macroscopic scales, the average is typically small compared with macroscopic scales, the average velocity of such a molecule has the form velocity of such a molecule has the form is a numerical constant on the order of is a numerical constant on the order of . (Some authors estimate . (Some authors estimate ;[16][32] on the other hand, a more careful calculation for rigid elastic spheres gives ;[16][32] on the other hand, a more careful calculation for rigid elastic spheres gives .) Now, because half the molecules on either side are moving towards .) Now, because half the molecules on either side are moving towards , and doing so on average with half theaverage moleculer speed , and doing so on average with half theaverage moleculer speed , the momentum flux from either side is , the momentum flux from either side is is the difference of the two: is the difference of the two: , which leads to , which leads to |
 and density
and density gives
gives
 is theBoltzmann constant,
is theBoltzmann constant, the molecular mass, and
the molecular mass, and a numerical constant on the order of
a numerical constant on the order of . The quantity
. The quantity , themean free path, measures the average distance a molecule travels between collisions. Even without a priori knowledge of
, themean free path, measures the average distance a molecule travels between collisions. Even without a priori knowledge of , this expression has interesting implications. In particular, since
, this expression has interesting implications. In particular, since is typically inversely proportional to density and increases with temperature,
is typically inversely proportional to density and increases with temperature, itself should increase with temperature and be independent of density at fixed temperature. In fact, both of these predictions persist in more sophisticated treatments, and accurately describe experimental observations. Note that this behavior runs counter to common intuition regarding liquids, for which viscosity typically decreases with temperature.[16][32]
itself should increase with temperature and be independent of density at fixed temperature. In fact, both of these predictions persist in more sophisticated treatments, and accurately describe experimental observations. Note that this behavior runs counter to common intuition regarding liquids, for which viscosity typically decreases with temperature.[16][32] ,
, can be computed, giving
can be computed, giving
 is independent of temperature, so
is independent of temperature, so . For more complicated molecular models, however,
. For more complicated molecular models, however, depends on temperature in a non-trivial way, and simple kinetic arguments as used here are inadequate. More fundamentally, the notion of a mean free path becomes imprecise for particles that interact over a finite range, which limits the usefulness of the concept for describing real-world gases.[33]
depends on temperature in a non-trivial way, and simple kinetic arguments as used here are inadequate. More fundamentally, the notion of a mean free path becomes imprecise for particles that interact over a finite range, which limits the usefulness of the concept for describing real-world gases.[33]Chapman–Enskog theory
 .[31] It is based on theBoltzmann equation, which provides a systematic statistical description of a dilute gas in terms of intermolecular interactions.[34] As such, their technique allows accurate calculation of
.[31] It is based on theBoltzmann equation, which provides a systematic statistical description of a dilute gas in terms of intermolecular interactions.[34] As such, their technique allows accurate calculation of for more realistic molecular models, such as those incorporating intermolecular attraction rather than just hard-core repulsion.
for more realistic molecular models, such as those incorporating intermolecular attraction rather than just hard-core repulsion. , which experiments show increases more rapidly than the
, which experiments show increases more rapidly than the trend predicted for rigid elastic spheres.[16] Indeed, the Chapman–Enskog analysis shows that the predicted temperature dependence can be tuned by varying the parameters in various molecular models. A simple example is the Sutherland model,[1] which describes rigid elastic spheres with weak mutual attraction. In such a case, the attractive force can be treatedperturbatively, which leads to a particularly simple expression for
trend predicted for rigid elastic spheres.[16] Indeed, the Chapman–Enskog analysis shows that the predicted temperature dependence can be tuned by varying the parameters in various molecular models. A simple example is the Sutherland model,[1] which describes rigid elastic spheres with weak mutual attraction. In such a case, the attractive force can be treatedperturbatively, which leads to a particularly simple expression for :
:
 is independent of temperature, being determined only by the parameters of the intermolecular attraction. To connect with experiment, it is convenient to rewrite as
is independent of temperature, being determined only by the parameters of the intermolecular attraction. To connect with experiment, it is convenient to rewrite as
 is the viscosity at temperature
is the viscosity at temperature .[35] If
.[35] If is known from experiments at
is known from experiments at and at least one other temperature, then
and at least one other temperature, then can be calculated. It turns out that expressions for
can be calculated. It turns out that expressions for obtained in this way are accurate for a number of gases over a sizable range of temperatures. On the other hand,Chapman & Cowling 1970argue that this success does not imply that molecules actually interact according to the Sutherland model. Rather, they interpret the prediction for
obtained in this way are accurate for a number of gases over a sizable range of temperatures. On the other hand,Chapman & Cowling 1970argue that this success does not imply that molecules actually interact according to the Sutherland model. Rather, they interpret the prediction for as a simple interpolation which is valid for some gases over fixed ranges of temperature, but otherwise does not provide a picture of intermolecular interactions which is fundamentally correct and general. Slightly more sophisticated models, such as theLennard-Jones potential, may provide a better picture, but only at the cost of a more opaque dependence on temperature. In some systems the assumption of spherical symmetry must be abandoned as well, as is the case for vapors with highlypolar moleculeslikeH2O.[36][37]
as a simple interpolation which is valid for some gases over fixed ranges of temperature, but otherwise does not provide a picture of intermolecular interactions which is fundamentally correct and general. Slightly more sophisticated models, such as theLennard-Jones potential, may provide a better picture, but only at the cost of a more opaque dependence on temperature. In some systems the assumption of spherical symmetry must be abandoned as well, as is the case for vapors with highlypolar moleculeslikeH2O.[36][37]Bulk viscosity
 for a monatomic ideal gas, in which the internal energy of molecules in negligible, but is nonzero for a gas likecarbon dioxide, whose molecules possess both rotational and vibrational energy.[38][39]
for a monatomic ideal gas, in which the internal energy of molecules in negligible, but is nonzero for a gas likecarbon dioxide, whose molecules possess both rotational and vibrational energy.[38][39]Pure liquids

Video showing three liquids with different viscosities

Experiment showing the behavior of a viscous fluid with blue dye for visibility
In contrast with gases, there is no simple yet accurate picture for the molecular origins of viscosity in liquids.
At the simplest level of description, the relative motion of adjacent layers in a liquid is opposed primarily by attractive molecular forces acting across the layer boundary. In this picture, one (correctly) expects viscosity to decrease with increasing temperature. This is because increasing temperature increases the random thermal motion of the molecules, which makes it easier for them to overcome their attractive interactions.[40]
Building on this visualization, a simple theory can be constructed in analogy with the discrete structure of a solid: groups of molecules in a liquid are visualized as forming "cages" which surround and enclose single molecules.[41] These cages can be occupied or unoccupied, and stronger molecular attraction corresponds to stronger cages. Due to random thermal motion, a molecule "hops" between cages at a rate which varies inversely with the strength of molecular attractions. In equilibrium these "hops" are not biased in any direction. On the other hand, in order for two adjacent layers to move relative to each other, the "hops" must be biased in the direction of the relative motion. The force required to sustain this directed motion can be estimated for a given shear rate, leading to
 | **(1)** |
 is theAvogadro constant,
is theAvogadro constant, is thePlanck constant,
is thePlanck constant, is the volume of amoleof liquid, and
is the volume of amoleof liquid, and is thenormal boiling point. This result has the same form as the widespread and accurate empirical relation
is thenormal boiling point. This result has the same form as the widespread and accurate empirical relation | **(2)** |
 and
and are constants fit from data.[41][42] On the other hand, several authors express caution with respect to this model.
Errors as large as 30% can be encountered using equation (**1), compared with fitting equation (2) to experimental data.[41] More fundamentally, the physical assumptions underlying equation (1) have been criticized.[43] It has also been argued that the exponential dependence in equation (1**) does not necessarily describe experimental observations more accurately than simpler, non-exponential expressions.[44][45]
are constants fit from data.[41][42] On the other hand, several authors express caution with respect to this model.
Errors as large as 30% can be encountered using equation (**1), compared with fitting equation (2) to experimental data.[41] More fundamentally, the physical assumptions underlying equation (1) have been criticized.[43] It has also been argued that the exponential dependence in equation (1**) does not necessarily describe experimental observations more accurately than simpler, non-exponential expressions.[44][45]In light of these shortcomings, the development of a less ad-hoc model is a matter of practical interest. Foregoing simplicity in favor of precision, it is possible to write rigorous expressions for viscosity starting from the fundamental equations of motion for molecules. A classic example of this approach is Irving-Kirkwood theory.[46] On the other hand, such expressions are given as averages over multiparticle correlation functions and are therefore difficult to apply in practice.
In general, empirically derived expressions (based on existing viscosity measurements) appear to be the only consistently reliable means of calculating viscosity in liquids.[47]
Mixtures and blends
Gaseous mixtures
 of a binary mixture of gases can be written in terms of the individual component viscosities
of a binary mixture of gases can be written in terms of the individual component viscosities , their respective volume fractions, and the intermolecular interactions.[31] As for the single-component gas, the dependence of
, their respective volume fractions, and the intermolecular interactions.[31] As for the single-component gas, the dependence of on the parameters of the intermolecular interactions enters through various collisional integrals which may not be expressible in terms of elementary functions. To obtain usable expressions for
on the parameters of the intermolecular interactions enters through various collisional integrals which may not be expressible in terms of elementary functions. To obtain usable expressions for which reasonably match experimental data, the collisional integrals typically must be evaluated using some combination of analytic calculation and empirical fitting. An example of such a procedure is the Sutherland approach for the single-component gas, discussed above.
which reasonably match experimental data, the collisional integrals typically must be evaluated using some combination of analytic calculation and empirical fitting. An example of such a procedure is the Sutherland approach for the single-component gas, discussed above.Blends of liquids
As for pure liquids, the viscosity of a blend of liquids is difficult to predict from molecular principles. One method is to extend the molecular "cage" theory presented above for a pure liquid. This can be done with varying levels of sophistication. One useful expression resulting from such an analysis is the Lederer-Roegiers equation for a binary mixture:

 is an empirical parameter, and
is an empirical parameter, and and
and are the respectivemole fractionsand viscosities of the component liquids.[48]
are the respectivemole fractionsand viscosities of the component liquids.[48]Since blending is an important process in the lubricating and oil industries, a variety of empirical and propriety equations exist for predicting the viscosity of a blend, besides those stemming directly from molecular theory.[48]
Solutions and suspensions
Aqeuous solutions
Depending on the solute and range of concentration, an aqueous electrolyte solution can have either a larger or smaller viscosity compared with pure water at the same temperature and pressure. For instance, a 20% saline (sodium chloride) solution has viscosity over 1.5 times that of pure water, whereas a 20% potassium iodide solution has viscosity about 0.91 times that of pure water.
 of a solution:[49]
of a solution:[49]
 is the viscosity of the solvent,
is the viscosity of the solvent, is the concentration, and
is the concentration, and is a positive constant which depends on both solvent and solute properties. However, this expression is only valid for very dilute solutions, having
is a positive constant which depends on both solvent and solute properties. However, this expression is only valid for very dilute solutions, having less than 0.1 mol/L.[50] For higher concentrations, additional terms are necessary which account for higher-order molecular correlations:
less than 0.1 mol/L.[50] For higher concentrations, additional terms are necessary which account for higher-order molecular correlations:
 and
and are fit from data. In particular, a negative value of
are fit from data. In particular, a negative value of is able to account for the decrease in viscosity observed in some solutions. Estimated values of these constants are shown below for sodium chloride and potassium iodide at temperature 25 °C (mol =mole, L =liter).[49]
is able to account for the decrease in viscosity observed in some solutions. Estimated values of these constants are shown below for sodium chloride and potassium iodide at temperature 25 °C (mol =mole, L =liter).[49]| Solute |  (mol-1/2L1/2) (mol-1/2L1/2) |  (mol−1L) (mol−1L) |  (mol−2L2) (mol−2L2) |
|---|---|---|---|
| Sodium chloride (NaCl) | 0.0062 | 0.0793 | 0.0080 |
| Potassium iodide (KI) | 0.0047 | −0.0755 | 0.0000 |
Suspensions
 can be defined in terms of stress and strain components which are averaged over a volume large compared with the distance between the suspended particles, but small with respect to macroscopic dimensions.[51] Such suspensions generally exhibit non-Newtonian behavior. However, for dilute systems in steady flows, the behavior is Newtonian and expressions for
can be defined in terms of stress and strain components which are averaged over a volume large compared with the distance between the suspended particles, but small with respect to macroscopic dimensions.[51] Such suspensions generally exhibit non-Newtonian behavior. However, for dilute systems in steady flows, the behavior is Newtonian and expressions for can be derived directly from the particle dynamics. In a very dilute system, with volume fraction
can be derived directly from the particle dynamics. In a very dilute system, with volume fraction , interactions between the suspended particles can be ignored. In such a case one can explicitly calculate the flow field around each particle independently, and combine the results to obtain
, interactions between the suspended particles can be ignored. In such a case one can explicitly calculate the flow field around each particle independently, and combine the results to obtain . For spheres, this results in the Einstein equation:
. For spheres, this results in the Einstein equation:
 is the viscosity of the suspending liquid. The linear dependence on
is the viscosity of the suspending liquid. The linear dependence on is a direct consequence of neglecting interparticle interactions; in general, one will have:
is a direct consequence of neglecting interparticle interactions; in general, one will have:
 may depend on the particle shape (e.g. spheres, rods, disks).[52] Experimental determination of the precise value of
may depend on the particle shape (e.g. spheres, rods, disks).[52] Experimental determination of the precise value of is difficult, however: even the prediction
is difficult, however: even the prediction for spheres has not been conclusively validated, with various experiments finding values in the range
for spheres has not been conclusively validated, with various experiments finding values in the range . This deficiency has been attributed to difficulty in controlling experimental conditions.[53]
. This deficiency has been attributed to difficulty in controlling experimental conditions.[53] acquires a nonlinear dependence on
acquires a nonlinear dependence on , which indicates the importance of interparticle interactions. Various analytical and semi-empirical schemes exist for capturing this regime. At the most basic level, a term quadratic in
, which indicates the importance of interparticle interactions. Various analytical and semi-empirical schemes exist for capturing this regime. At the most basic level, a term quadratic in is added to
is added to :
:
 is fit from experimental data or approximated from the microscopic theory. In general, however, one should be cautious in applying such simple formulas since non-Newtonian behavior appears in dense suspensions (
is fit from experimental data or approximated from the microscopic theory. In general, however, one should be cautious in applying such simple formulas since non-Newtonian behavior appears in dense suspensions ( for spheres),[53] or in suspensions of elongated or flexible particles.[51]
for spheres),[53] or in suspensions of elongated or flexible particles.[51]There is a distinction between a suspension of solid particles, described above, and an emulsion. The latter is a suspension of tiny droplets, which themselves may exhibit internal circulation. The presence of internal circulation can noticeably decrease the observed effective viscosity, and different theoretical or semi-empirical models must be used.[54]
Amorphous materials
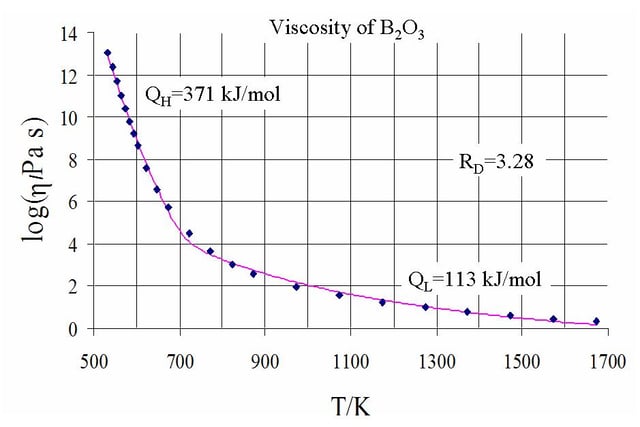
Common logarithm of viscosity against temperature for B2O3, showing two regimes

where Q is a relevant activation energy, given in terms of molecular parameters; T is temperature; R is the molar gas constant; and A is approximately a constant. The activation energy Q takes a different value depending on whether the high or low temperature limit is being considered: it changes from a high value QH at low temperatures (in the glassy state) to a low value QL at high temperatures (in the liquid state).
 varies nontrivially with temperature and the simple Arrhenius form fails. On the other hand, the two-exponential equation
varies nontrivially with temperature and the simple Arrhenius form fails. On the other hand, the two-exponential equation![{\displaystyle \mu =AT\exp \left({\frac {B}{RT}}\right)\left[1+C\exp \left({\frac {D}{RT}}\right)\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38aa9224e9ac73624655cd20405e140af63a62eb)
 ,
, ,
, ,
, are all constants, provides a good fit to experimental data over the entire range of temperatures, while at the same time reducing to the correct Arrhenius form in the low and high temperature limits. Besides being a convenient fit to data, the expression can also be derived from various theoretical models of amorphous materials at the atomic level.[57]
are all constants, provides a good fit to experimental data over the entire range of temperatures, while at the same time reducing to the correct Arrhenius form in the low and high temperature limits. Besides being a convenient fit to data, the expression can also be derived from various theoretical models of amorphous materials at the atomic level.[57]Eddy viscosity
In the study of turbulence in fluids, a common practical strategy is to ignore the small-scale vortices (or eddies) in the motion and to calculate a large-scale motion with an effective viscosity, called the "eddy viscosity", which characterizes the transport and dissipation of energy in the smaller-scale flow (see large eddy simulation).[59][60] In contrast to the viscosity of the fluid itself, which must be positive by the second law of thermodynamics, the eddy viscosity can be negative.[61][62]
Selected substances

In the University of Queensland pitch drop experiment, pitch has been dripping slowly through a funnel since 1927, at a rate of one drop roughly every decade. In this way the viscosity of pitch has been determined to be approximately 230 billion (2.3×1011) times that of water.[63]
Observed values of viscosity vary over several orders of magnitude, even for common substances (see the order of magnitude table below). For instance, a 70% sucrose (sugar) solution has a viscosity over 400 times that of water, and 26000 times that of air.[64] More dramatically, pitch has been estimated to have a viscosity 230 billion times that of water.[63]
Water
 ofwateris about 0.89 mPa·s at room temperature (25 °C). As a function of temperature inkelvins, the viscosity can be estimated using the semi-empirical relation
ofwateris about 0.89 mPa·s at room temperature (25 °C). As a function of temperature inkelvins, the viscosity can be estimated using the semi-empirical relation
where A = 0.02939 mPa·s, B = 507.88 K, and C = 149.3 K.[65] Experimentally determined values of the viscosity are also given in the table below.
| Temperature (°C) | Viscosity (mPa·s) |
|---|---|
| 10 | 1.3059 |
| 20 | 1.0016 |
| 30 | 0.79722 |
| 50 | 0.54652 |
| 70 | 0.40355 |
| 90 | 0.31417 |
Air

Honey being drizzled
Under standard atmospheric conditions (25 °C and pressure of 1 bar), the dynamic viscosity of air is 18.5 μPa·s, roughly 50 times smaller than the viscosity of water at the same temperature. Except at very high pressure, the viscosity of air depends mostly on the temperature.
Other common substances
Order of magnitude estimates
The following table illustrates the range of viscosity values observed in common substances. Unless otherwise noted, a temperature of 25 °C and a pressure of 1 atmosphere are assumed. Certain substances of variable composition or with non-Newtonian behavior are not assigned precise values, since in these cases viscosity depends on additional factors besides temperature and pressure.
| Factor (Pa·s) | Description | Examples | Values (Pa·s) | Ref. |
|---|---|---|---|---|
| 10−6 | Lower range of gaseous viscosity | Butane | 7.49 × 10−6 | [70] |
| Hydrogen | 8.8 × 10−6 | [71] | ||
| 10−5 | Upper range of gaseous viscosity | Krypton | 2.538 × 10−5 | [72] |
| Neon | 3.175 × 10−5 | |||
| 10−4 | Lower range of liquid viscosity | Pentane | 2.24 × 10−4 | [64] |
| Gasoline | 6 × 10−4 | |||
| Water | 8.90 × 10−4 | [64] | ||
| 10−3 | Typical range for small-molecule Newtonian liquids | Ethanol | 1.074 × 10−3 | |
| Mercury | 1.526 × 10−3 | |||
| Whole milk (20 °C) | 2.12 × 10−3 | [66] | ||
| Blood | 4 × 10−3 | |||
| 10−2– 100 | Oils and long-chain hydrocarbons | Linseed oil | 0.028 | |
| Olive oil | 0.084 | [66] | ||
| SAE 10 Motor oil | 0.085 to 0.14 | |||
| Castor oil | 0.1 | |||
| SAE 20 Motor oil | 0.14 to 0.42 | |||
| SAE 30 Motor oil | 0.42 to 0.65 | |||
| SAE 40 Motor oil | 0.65 to 0.90 | |||
| Glycerine | 1.5 | |||
| Pancake syrup | 2.5 | |||
| 101– 103 | Pastes, gels, and other semisolids (generally non-Newtonian) | Ketchup | ≈ 101 | [68] |
| Mustard | ||||
| Sour cream | ≈ 102 | |||
| Peanut butter | [69] | |||
| Lard | ≈ 103 | |||
| ≈108 | Viscoelastic polymers | Pitch | [63] | |
| ≈1021 | Certain solids under a viscoelastic description | Mantle (geology) |
See also
Dashpot
Deborah number
Dilatant
Herschel–Bulkley fluid
Hyperviscosity syndrome
Intrinsic viscosity
Inviscid flow
Joback method (estimation of liquid viscosity from molecular structure)
Kaye effect
Microviscosity
Morton number
Quasi-solid
Rheology
Stokes flow
Superfluid helium-4
Viscoplasticity
Viscosity models for mixtures