En geometría analítica y álgebra elemental, una función afín (lineal) es una función polinómica de primer grado, es decir, una función cuya representación en el plano cartesiano es una línea recta.

Esta función se puede escribir como: f(x)=mx+b

Donde m yb son constantes reales y x es una variable real.

La constante m determina la pendiente o inclinación de la recta, y la constante b determina el punto de corte de la recta con el eje vertical o eje de las ordenadas y en el sistema de coordenadas cartesianas.

La función afín es también conocida como transformación lineal, en el contexto de álgebra lineal.

Y en el contexto del análisis matemático la función afín f(x)=mx con b=0 recibe el nombre de función lineal.

Una función lineal de una única variable dependiente x es de la forma:

y=mx+b

Es la ecuación de una recta en el plano xy.

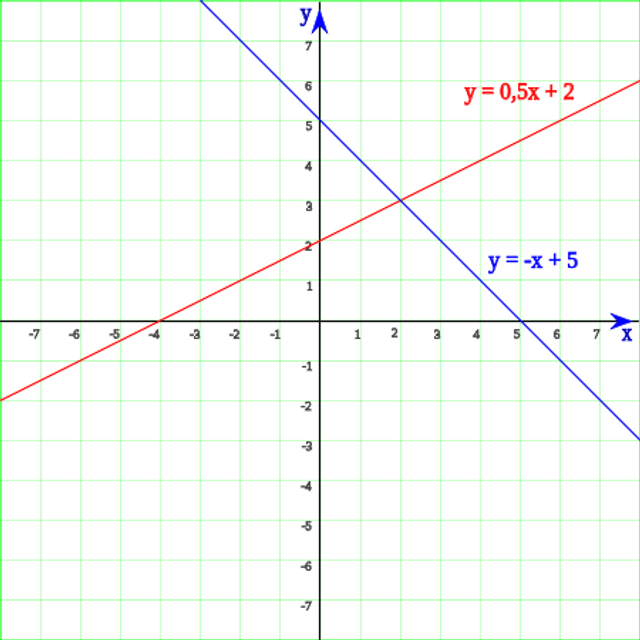
En la figura se ven dos rectas, que corresponden a las ecuaciones lineales siguientes:

y=0,5x+2}

En esta recta el parámetrom=0.5=1/2 (corresponde al valor de la pendiente de la recta), Este valor corresponde a la razón de cambio de la ordenaday por cada cambio en una unidad en la abscisa x.

Es decir, en el caso particular del ejemplo, cuando aumentamos x en una unidad entonces y aumenta en 1/2 por esa unidad más el valor constante b =2.

Esto corresponde al punto de coordenadas (1, 2.5)

Como b=0 entonces la recta pasa por el punto donde la x=0 y la y=2.

Esto es el punto (0,2)

En la gráfica se ve ve que la segunda recta, la identificada con el color azul pasa por los puntos (0,5) y (5,0).

Conocidos los puntos por donde pasa la recta el objetivo que se persigue es conseguir su ecuación.

Dados dos puntos P=(x, y) y P'=(x',y') por donde pasa la recta permite conocer la pendiente m mediante la formula siguiente**:**

m=y'-y/x'-x

En el caso del ejemplo que se ha venido planteandom=0-5/5-0=-5/5=-1

La pendiente negativa indica que la razón de cambio es un proceso decreciente.

La recta decrece a razón de una unidad más la constanteb por cada cambio en la abscisa x. Se debe recordar que b corresponde a la intersección de la recta con el eje de las ordenadas y (esto es cuando x=0). En el ejemplo tratado b=5.

Existen varias ecuaciones de la recta, pero en este caso especial será considerada la ecuación Pendiente Intersección con el Eje de las Ordenadas Y (EPI).

Esta es: y=mx+b

Continuando en la **** de la ecuación de la recta identificada con el color azul en la imagen, y conociendo los valores dem=-1 yb=5, su ecuación viene dada por y=-x+5.