Quaternion
Quaternion

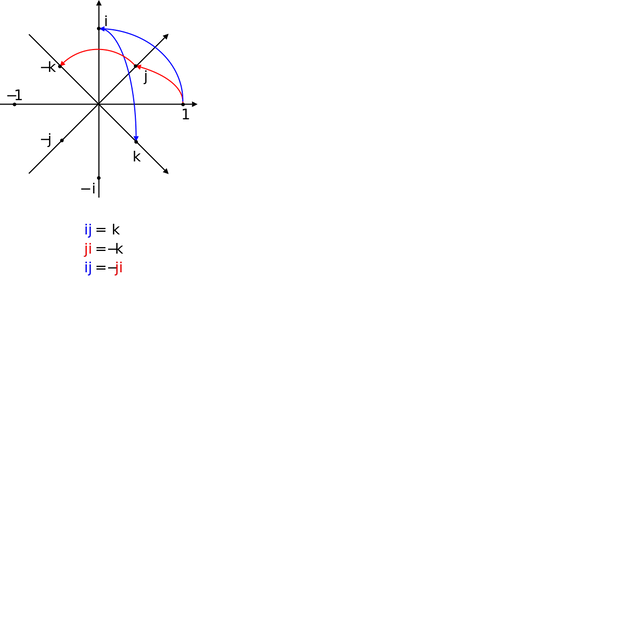
| × | 1 | i | j | k |
|---|---|---|---|---|
| 1 | 1 | i | j | k |
| i | i | −1 | k | −j |
| j | j | −k | −1 | i |
| k | k | j | −i | −1 |
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician William Rowan Hamilton in 1843[3][4] and applied to mechanics in three-dimensional space. A feature of quaternions is that multiplication of two quaternions is noncommutative. Hamilton defined a quaternion as the quotient of two directed lines in a three-dimensional space[5] or equivalently as the quotient of two vectors.[6]
Quaternions are generally represented in the form:
where a, b, c, and d are real numbers, and i, j, and k are the fundamental quaternion units.
Quaternions find uses in both pure and applied mathematics, in particular for calculations involving three-dimensional rotations such as in three-dimensional computer graphics, computer vision, and crystallographic texture analysis.[7] In practical applications, they can be used alongside other methods, such as Euler angles and rotation matrices, or as an alternative to them, depending on the application.
The unit quaternions can be thought of as a choice of a group structure on the 3-sphere S3 that gives the group Spin(3), which is isomorphic to SU(2) and also to the universal cover of SO(3).
History

Quaternion plaque on Brougham (Broom) Bridge, Dublin, which says: Here as he walked byon the 16th of October 1843Sir William Rowan Hamiltonin a flash of genius discoveredthe fundamental formula forquaternion multiplication i2 = j2 = k2 = ijk = −1& cut it on a stone of this bridge
Quaternions were introduced by Hamilton in 1843.[9] Important precursors to this work included Euler's four-square identity (1748) and Olinde Rodrigues' parameterization of general rotations by four parameters (1840), but neither of these writers treated the four-parameter rotations as an algebra.[10][11] Carl Friedrich Gauss had also discovered quaternions in 1819, but this work was not published until 1900.[12][13]
Hamilton knew that the complex numbers could be interpreted as points in a plane, and he was looking for a way to do the same for points in three-dimensional space. Points in space can be represented by their coordinates, which are triples of numbers, and for many years he had known how to add and subtract triples of numbers. However, Hamilton had been stuck on the problem of multiplication and division for a long time. He could not figure out how to calculate the quotient of the coordinates of two points in space.
The great breakthrough in quaternions finally came on Monday 16 October 1843 in Dublin, when Hamilton was on his way to the Royal Irish Academy where he was going to preside at a council meeting. As he walked along the towpath of the Royal Canal with his wife, the concepts behind quaternions were taking shape in his mind. When the answer dawned on him, Hamilton could not resist the urge to carve the formula for the quaternions,
into the stone of Brougham Bridge as he paused on it. Although the carving has since faded away, there has been an annual pilgrimage since 1989 called the Hamilton Walk for scientists and mathematicians who walk from Dunsink Observatory to the Royal Canal bridge in remembrance of Hamilton's discovery.
On the following day, Hamilton wrote a letter to his friend and fellow mathematician, John T. Graves, describing the train of thought that led to his discovery.
This letter was later published in a letter to a science magazine;[14] Hamilton states:
And here there dawned on me the notion that we must admit, in some sense, a fourth dimension of space for the purpose of calculating with triples...
An electric circuit seemed to close, and a spark flashed forth.[14]
Hamilton called a quadruple with these rules of multiplication a quaternion, and he devoted most of the remainder of his life to studying and teaching them. Hamilton's treatment is more geometric than the modern approach, which emphasizes quaternions' algebraic properties. He founded a school of "quaternionists", and he tried to popularize quaternions in several books. The last and longest of his books, Elements of Quaternions,[15] was 800 pages long; it was edited by his son and published shortly after his death.
After Hamilton's death, his student Peter Tait continued promoting quaternions. At this time, quaternions were a mandatory examination topic in Dublin. Topics in physics and geometry that would now be described using vectors, such as kinematics in space and Maxwell's equations, were described entirely in terms of quaternions. There was even a professional research association, the Quaternion Society, devoted to the study of quaternions and other hypercomplex number systems.
From the mid-1880s, quaternions began to be displaced by vector analysis, which had been developed by Josiah Willard Gibbs, Oliver Heaviside, and Hermann von Helmholtz. Vector analysis described the same phenomena as quaternions, so it borrowed some ideas and terminology liberally from the literature on quaternions. However, vector analysis was conceptually simpler and notationally cleaner, and eventually quaternions were relegated to a minor role in mathematics and physics. A side-effect of this transition is that Hamilton's work is difficult to comprehend for many modern readers. Hamilton's original definitions are unfamiliar and his writing style was wordy and difficult to understand.
However, quaternions have had a revival since the late 20th century, primarily due to their utility in describing spatial rotations. The representations of rotations by quaternions are more compact and quicker to compute than the representations by matrices. In addition, unlike Euler angles, they are not susceptible to “gimbal lock”. For this reason, quaternions are used in computer graphics,[16][17] computer vision, robotics,[18] control theory, signal processing, attitude control, physics, bioinformatics,[19][20] molecular dynamics, computer simulations, and orbital mechanics. For example, it is common for the attitude control systems of spacecraft to be commanded in terms of quaternions. Quaternions have received another boost from number theory because of their relationships with the quadratic forms.[21]
Quaternions in physics
P.R.
Girard's 1984 essay The quaternion group and modern physics [22] discusses some roles of quaternions in physics. The essay
shows how various physical covariance groups: SO(3), the Lorentz group, the general theory of relativity group, the Clifford algebra SU(2) and the conformal group can easily be related to the quaternion group
in modern algebra. Girard began by discussing group representations and by representing some space groups of crystallography. He proceeded to kinematics of rigid body motion. Next he used complex quaternions (biquaternions) to represent the Lorentz group of special relativity, including the Thomas precession. He cited five authors, beginning with Ludwik Silberstein, who used a potential function of one quaternion variable to express Maxwell's equations in a single differential equation. Concerning general relativity, he expressed the Runge–Lenz vector. He mentioned the Clifford biquaternions (split-biquaternions) as an instance of Clifford algebra. Finally, invoking the reciprocal of a biquaternion, Girard described conformal maps on spacetime. Among the fifty references, Girard included Alexander Macfarlane and his Bulletin of the Quaternion Society. In 1999 he showed how Einstein's equations of general relativity could be formulated within a Clifford algebra that is directly linked to quaternions.[23]
The finding of 1924 that in quantum mechanics the spin of an electron and other matter particles (known as spinors) can be described using quaternions furthered their interest; quaternions helped to understand how rotations of electrons by 360° can be discerned from those by 720° (the “Plate trick”).[24][25] As of 2018, their use has not overtaken rotation groups.[1]
Definition
A quaternion is an expression of the form
where a, b, c, d, are real numbers, and i, j, k, are symbols that can be interpreted as unit-vectors pointing along the three spatial axes. In practice, if one of a, b, c, d is 0, the corresponding term is omitted; if a, b, c, d are all zero, the quaternion is the zero quaternion, denoted 0; if one of b, c, d equals 1, the corresponding term is written simply i, j, or k.
and the componentwise scalar multiplication
A multiplicative group structure, called the Hamilton product, denoted by juxtaposition, can be defined on the quaternions in the following way:
The real quaternion 1 is the identity element.
The real quaternions commute with all other quaternions, that is aq = qa for every quaternion q and every real quaternion a. In algebraic terminology this is to say that the field of real quaternions are the center of this quaternion algebra.
The product is first given for the basis elements (see next subsection), and then extended to all quaternions by using the distributive property and the center property of the real quaternions. The Hamilton product is not commutative, but associative, thus the quaternions form an associative algebra over the reals.
Additionally, every nonzero quaternion has an inverse with respect to the Hamilton product:
Thus the quaternions form a division algebra.
Multiplication of basis elements
| × | 1 | i | j | k |
|---|---|---|---|---|
| 1 | 1 | i | j | k |
| i | i | −1 | k | −j |
| j | j | −k | −1 | i |
| k | k | j | −i | −1 |
The basis elements i, j, and k commute with the real quaternion 1, that is
The other products of basis elements are defined by
and
These multiplication formulas are equivalent to
In fact, the equality ijk = –1 results from
The converse implication results from manipulations similar to the following.
By right-multiplying both sides of −1 = ijk by –k, one gets
All other products can be determined by similar methods.
Center
The center of a noncommutative ring is the subring of elements c such that cx = xc for every x. The center of the quaternion algebra is the subfield of real quaternions. In fact, it is a part of the definition that the real quaternions belong to the center. Conversely, if q = a + bi + cj + dk belongs to the center, then
and c = d = 0. A similar computation with j instead of i shows that one has also b = 0. Thus q = a is a real quaternion.
The quaternion form a division algebra. This means that the noncommutativity of multiplication is the only property that makes quaternions different from a field. This noncommutativity has some unexpected consequences, among them that a polynomial equation over the quaternions can have more distinct solutions than the degree of the polynomial. For example, the equation z2 + 1 = 0, has infinitely many quaternion solutions, which are the quaternions z = bi + cj + dk such that b2 + c2 + d2 = 1. Thus these "roots of –1" form a unit sphere in the three-dimensional space of vector quaternions.
Hamilton product
For two elements a1 + b1i + c1j + d1k and a2 + b2i + c2j + d2k, their product, called the Hamilton product (a1 + b1i + c1j + d1k) (a2 + b2i + c2j + d2k), is determined by the products of the basis elements and the distributive law. The distributive law makes it possible to expand the product so that it is a sum of products of basis elements. This gives the following expression:
Now the basis elements can be multiplied using the rules given above to get:[9]
The product of two rotation quaternions[26] will be equivalent to the rotation a2 + b2i + c2j + d2k followed by the rotation a1 + b1i + c1j + d1k.
Scalar and vector parts
A quaternion of the form a + 0i + 0j + 0k, where a is a real number, is called scalar, and a quaternion of the form 0 + bi + cj + dk, where b, c, and d are real numbers, and at least one of b, c or d is nonzero, is called a vector quaternion. If a + bi + cj + dk is any quaternion, then a is called its scalar part and bi + cj + dk is called its vector part. Even though every quaternion can be viewed as a vector in a four-dimensional vector space, it is common to refer to the vector part as vectors in three-dimensional space. With this convention, a vector is the same as an element of the vector space R 3.[2]
If a quaternion is divided up into a scalar part and a vector part, i.e.
then the formulas for addition and multiplication are:
where "·" is the dot product and "×" is the cross product.
Conjugation, the norm, and reciprocal
The conjugation of a quaternion, in stark contrast to the complex setting, can be expressed with multiplication and addition of quaternions:
Conjugation can be used to extract the scalar and vector parts of a quaternion.
The scalar part of p is (p + p∗) / 2, and the vector part of p is (p − p∗) / 2.
The square root of the product of a quaternion with its conjugate is called itsnorm and is denoted ||qtensor* of q g of "tensor"). In formula, this is expressed as follows:
This is always a non-negative real number, and it is the same as the Euclidean norm on H considered as the vector space R 4. Multiplying a quaternion by a real number scales its norm by the absolute value of the number. That is, if α is real, then
This is a special case of the fact that the norm is multiplicative, meaning that
for any two quaternions p and q. Multiplicativity is a consequence of the formula for the conjugate of a product. Alternatively it follows from the identity
(where i denotes the usual imaginary unit) and hence from the multiplicative property of determinants of square matrices.
This norm makes it possible to define the distance d (p, q) between p and q as the norm of their difference:
This makes H a metric space. Addition and multiplication are continuous in the metric topology. Indeed, for any scalar, positive a it holds
Continuity follows from taking a to zero in the limit. Continuity for multiplication holds similarly.
Unit quaternion
A unit quaternion is a quaternion of norm one. Dividing a non-zero quaternion q by its norm produces a unit quaternion U qcalled the versor
This makes it possible to divide two quaternions p and q in two different ways (when q is non-zero). That is, their quotient can be either p q−1 or q−1p. The notation p/q is ambiguous because it does not specify whether q divides on the left or the right.
Algebraic properties

Cayley graph of Q8. The red arrows represent multiplication on the right by i, and the green arrows represent multiplication on the right by j.

Three dimensional graph of Q8.
The set H of all quaternions is a vector space over the real numbers with dimension 4. (In comparison, the real numbers have dimension 1, the complex numbers have dimension 2, and the octonions have dimension 8.) Multiplication of quaternions is associative and distributes over vector addition, but it is not commutative. Therefore, the quaternions H are a non-commutative associative algebra over the real numbers. Even though H contains copies of the complex numbers, it is not an associative algebra over the complex numbers.
Because it is possible to divide quaternions, they form a division algebra. This is a structure similar to a field except for the non-commutativity of multiplication. Finite-dimensional associative division algebras over the real numbers are very rare. The Frobenius theorem states that there are exactly three: R, C, and H. The norm makes the quaternions into a normed algebra, and normed division algebras over the reals are also very rare: Hurwitz's theorem says that there are only four: R, C, H, and O (the octonions). The quaternions are also an example of a composition algebra and of a unital Banach algebra.
Because the product of any two basis vectors is plus or minus another basis vector, the set {±1, ±i, ±, ±k*} forms a group under multiplication. This non-Abelian Group is called the quaternion group and is denoted Q8.[29] The real group ring of Q8 is a ring R [Q8] which is also an eight-dimensional vector space over R. It has one basis vector for each element of Q8. The quaternions are the quotient ring of R [Q8] by the ideal generated by the elements 1 + (−1), i+ (−), j*+ (−j), and* k*+ (−k). Here the first term in each of the differences is one of the basis elements 1,* i*,* j*, and* k*, and the second term is one of basis elements −1, −i, −j, and −k, not the additive inverses of 1,* i*,* j*, and* k*.
Quaternions and the geometry of R3
The vector part of a quaternion can be interpreted as a coordinate vector in R 3; therefore, the algebraic operations of the quaternions reflect the geometry of R 3. Operations such as the vector dot and cross products can be defined in terms of quaternions, and this makes it possible to apply quaternion techniques wherever spatial vectors arise. A useful application of quaternions has been to interpolate the orientations of key-frames in computer graphics.[16]
For the remainder of this section, i, j, and kl denote both the three imaginary[30] basis vectors of H and a basis for R 3. Replacing i by −*, jby −j, and* kby −ksends a vector to its additive inverse, so the additive inverse of a vector is the same as its conjugate as a quaternion. For this reason, conjugation is sometimes called the spatial inverse*.
For two vector quaternions p = b1i + c1j + d1k and q = b2i + c2j + d2k their dot product, by analogy to vectors in R 3, is
It can also be expressed in a component-free manner as
This is equal to the scalar parts of the products pq∗, qp∗, p∗, and q∗p*. Note that their vector parts are different.
The cross product of p and q relative to the orientation determined by the ordered basis i, j, and k is
(Recall that the orientation is necessary to determine the sign.) This is equal to the vector part of the product pq (as quaternions), as well as the vector part of −q∗p∗. It also has the formula
For the commutator, [p,* q*] =* pq− qp*, of two vector quaternions one obtains
In general, let p and q be quaternions and write
This shows that the noncommutativity of quaternion multiplication comes from the multiplication of vector quaternions.
It also shows that two quaternions commute if and only if their vector parts are collinear.
Hamilton[31] showed that this product computes the third vertex of a spherical triangle from two given vertices and their associated arc-lengths, which is also an algebra of points in Elliptic geometry.
See Andrew J. Hanson.[32] for visualization of quaternions.
Matrix representations
Just as complex numbers can be represented as matrices, so can quaternions. There are at least two ways of representing quaternions as matrices in such a way that quaternion addition and multiplication correspond to matrix addition and matrix multiplication. One is to use 2 × 2 complex matrices, and the other is to use 4 × 4 real matrices. In each case, the representation given is one of a family of linearly related representations. In the terminology of abstract algebra, these are injective homomorphisms from H to the matrix rings M(2, C) and M(4, R), respectively.
Using 2 × 2 complex matrices, the quaternion a + bi + cj + dk can be represented as
This representation has the following properties:
Constraining any two of b, c and d to zero produces a representation of complex numbers. For example, setting c = d = 0 produces a diagonal complex matrix representation of complex numbers, and setting b = d = 0 produces a real matrix representation.
The norm of a quaternion (the square root of the product with its conjugate, as with complex numbers) is the square root of the determinant of the corresponding matrix.[33]
The conjugate of a quaternion corresponds to the conjugate transpose of the matrix.
By restriction this representation yields an isomorphism between the subgroup of unit quaternions and their image SU(2). Topologically, the unit quaternions are the 3-sphere, so the underlying space of SU(2) is also a 3-sphere. The group SU(2) is important for describing spin in quantum mechanics; see Pauli matrices.
There is a strong relation between quaternion units and Pauli matrices.
Obtain the eight quaternion unit matrices by taking a, b, c and d, set three of them at zero and the fourth at 1 or −1. Multiplying any two Pauli matrices always yields a quaternion unit matrix, all of them except for −1. One obtains −1 via i2 = j2 = k2 = ijk = −1. E.g. the last equality is
Using 4 × 4 real matrices, that same quaternion can be written as
However, the representation of quaternions in M(4,ℝ) is not unique.
For example, the same quaternion can also be represented as
In fact, there exist 48 distinct representations of this form.
More precisely, there are 48 sets of quadruples of matrices such that a function sending 1, i, j, and k to the matrices in the quadruple is a homomorphism, that is, it sends sums and products of quaternions to sums and products of matrices.[34] In this representation, the conjugate of a quaternion corresponds to the transpose of the matrix. The fourth power of the norm of a quaternion is the determinant of the corresponding matrix. As with the 2 × 2 complex representation above, complex numbers can again be produced by constraining the coefficients suitably; for example, as block diagonal matrices with two 2 × 2 blocks by setting c = d = 0.
Each 4x4 matrix representation of quaternions corresponds to a multiplication table of unit quaternions.
For example, the last matrix representation given above corresponds to the multiplication table
| × | a | d | −b | −c |
|---|---|---|---|---|
| a | a | d | −b | −c |
| −d | −d | a | c | −b |
| b | b | −c | a | −d |
| c | c | b | d | a |
| × | 1 | k | −i | −j |
|---|---|---|---|---|
| 1 | 1 | k | −i | −j |
| −k | −k | 1 | j | −i |
| i | i | −j | 1 | −k |
| j | j | i | k | 1 |
Constraining any such multiplication table to have the identity in the first row and column and for the signs of the row headers to be opposite to those of the column headers, then there are 3 possible choices for the second column (ignoring sign), 2 possible choices for the third column (ignoring sign), and 1 possible choice for the fourth column (ignoring sign); that makes 6 possibilities.
Then, the second column can be chosen to be either positive or negative, the third column can be chosen to be positive or negative, and the fourth column can be chosen to be positive or negative, giving 8 possibilities for the sign.
Multiplying the possibilities for the letter positions and for their signs yields 48.
Then replacing 1 with a, i with b, j with c, and k with d and removing the row and column headers yields a matrix representation of a + bi + cj + dk.
Lagrange’s four square theorem
Quaternions are also used in one of the proofs of Lagrange's four-square theorem in number theory, which states that every nonnegative integer is the sum of four integer squares. As well as being an elegant theorem in its own right, Lagrange's four square theorem has useful applications in areas of mathematics outside number theory, such as combinatorial design theory. The quaternion-based proof uses Hurwitz quaternions, a subring of the ring of all quaternions for which there is an analog of the Euclidean algorithm.
Quaternions as pairs of complex numbers
Quaternions can be represented as pairs of complex numbers.
From this perspective, quaternions are the result of applying the Cayley–Dickson construction to the complex numbers. This is a generalization of the construction of the complex numbers as pairs of real numbers.
Let C 2 be a two-dimensional vector space over the complex numbers. Choose a basis consisting of two elements 1 and j. A vector in C 2 can be written in terms of the basis elements 1 and j as
If we define j2 = −1 and ij = −ji, then we can multiply two vectors using the distributive law. Writing* kin place of the product ijleads to the same rules for multiplication as the usual quaternions. Therefore, the above vector of complex numbers corresponds to the quaternion a*+* bi*+* cj*+* dk*. If we write the elements of* C 2 as ordered pairs and quaternions as quadruples, then the correspondence is
Square roots of −1
In the complex numbers, C, there are just two numbers, i and −i, whose square is −1. In* H there are infinitely many square roots of minus one: the quaternion solution for the square root of −1 is the unit sphere in R 3. To see this, let q = a + bi + cj + dk be a quaternion, and assume that its square is −1. In terms of a, b, c, and d, this means
To satisfy the last three equations, either a = 0 or b, c, and d are all 0. The latter is impossible because a is a real number and the first equation would imply that a2 = −1. Therefore, a = 0 and b2 + c2 + d2 = 1. In other words: a quaternion squares to −1 if and only if it is a vector quaternion with norm 1. By definition, the set of all such vectors forms the unit sphere.
Only negative real quaternions have infinitely many square roots.
All others have just two (or one in the case of 0).
The identification of the square roots of minus one in H was given by Hamilton[35] but was frequently omitted in other texts. By 1971 the sphere was included by Sam Perlis in his three-page exposition included in Historical Topics in Algebra (page 39) published by the National Council of Teachers of Mathematics. More recently, the sphere of square roots of minus one is described in Ian R. Porteous's book Clifford Algebras and the Classical Groups (Cambridge, 1995) in proposition 8.13 on page 60.
H as a union of complex planes
Each pair of square roots of −1 creates a distinct copy of the complex numbers inside the quaternions.
If q2 = −1, then the copy is determined by the function
In the language of abstract algebra, each is an injective ring homomorphism from C to H. The images of the embeddings corresponding to q and −q are identical.
Every non-real quaternion determines a planar subspace in H that is isomorphic to C: Write q as the sum of its scalar part and its vector part:
Decompose the vector part further as the product of its norm and its versor:
Commutative subrings
The relationship of quaternions to each other within the complex subplanes of H can also be identified and expressed in terms of commutative subrings. Specifically, since two quaternions p and q commute (i.e., pq = qp) only if they lie in the same complex subplane of H, the profile of H as a union of complex planes arises when one seeks to find all commutative subrings of the quaternion ring. This method of commutative subrings is also used to profile the split-quaternions, which as an algebra over the reals are isomorphic to 2 × 2 real matrices.
Functions of a quaternion variable

The Julia sets and Mandelbrot sets can be extended to the Quaternions, but they must use cross sections to be rendered visually in 3 dimensions.
Like functions of a complex variable, functions of a quaternion variable suggest useful physical models. For example, the original electric and magnetic fields described by Maxwell were functions of a quaternion variable. Examples of other functions include the extension of the Mandelbrot set and Julia sets into 4 dimensional space.[36]
Exponential, logarithm, and power functions
Given a quaternion,
the exponential is computed as
- .[37]
It follows that the polar decomposition of a quaternion may be written
and
Geodesic norm
The geodesic distance dg (p, q) between unit quaternions p and q is defined as:
and amounts to the absolute value of half the angle subtended by p and q along a great arc of the S3 sphere. This angle can also be computed from the quaternion dot product without the logarithm as:
Three-dimensional and four-dimensional rotation groups
The word "conjugation", besides the meaning given above, can also mean taking an element a to r a r−1 where r is some non-zero quaternion. All elements that are conjugate to a given element (in this sense of the word conjugate) have the same real part and the same norm of the vector part. (Thus the conjugate in the other sense is one of the conjugates in this sense.)
Thus the multiplicative group of non-zero quaternions acts by conjugation on the copy of R 3 consisting of quaternions with real part equal to zero. Conjugation by a unit quaternion (a quaternion of absolute value 1) with real part cos(φ) is a rotation by an angle 2φ, the axis of the rotation being the direction of the vector part. The advantages of quaternions are:
Avoiding gimbal lock, a problem with systems such as Euler angles.
Faster and more compact than matrices.
Nonsingular representation (compared with Euler angles for example).
Pairs of unit quaternions represent a rotation in 4D space (see Rotations in 4-dimensional Euclidean space: Algebra of 4D rotations
The set of all unit quaternions (versors) forms a 3-sphere S3 and a group (a Lie group) under multiplication, double covering the group SO(3, R) of real orthogonal 3×3 matrices of determinant 1 since two unit quaternions correspond to every rotation under the above correspondence. See the plate trick.
The image of a subgroup of versors is a point group, and conversely, the preimage of a point group is a subgroup of versors. The preimage of a finite point group is called by the same name, with the prefix binary. For instance, the preimage of the icosahedral group is the binary icosahedral group.
The versors' group is isomorphic to SU(2), the group of complex unitary 2×2 matrices of determinant 1.
Let A be the set of quaternions of the form a + bi + cj + dk where a, b, c, and d are either all integers or all rational numbers with odd numerator and denominator 2. The set A is a ring (in fact a domain) and a lattice and is called the ring of Hurwitz quaternions. There are 24 unit quaternions in this ring, and they are the vertices of a regular 24-cell with Schläfli symbol {3,4,3}. They correspond to the double cover of the rotational symmetry group of the regular tetrahedron. Similarly, the vertices of a regular 600-cell with Schläfli symbol {3,3,5} can be taken as the unit icosians, corresponding to the double cover of the rotational symmetry group of the regular icosahedron. The double cover of the rotational symmetry group of the regular octahedron corresponds to the quaternions that represent the vertices of the disphenoidal 288-cell.
Quaternion algebras
The Quaternions can be generalized into further algebras called quaternion algebras. Take F to be any field with characteristic different from 2, and a and b to be elements of F; a four-dimensional unitary associative algebra can be defined over F with basis 1, i, j, and ij, where i2 = a, j2 = b and ij = −ji (so* (ij)2 = −ab*).
Quaternion algebras are isomorphic to the algebra of 2×2 matrices over F or form division algebras over F, depending on the choice of a and b.
Quaternions as the even part of Cℓ3,0(R)
The usefulness of quaternions for geometrical computations can be generalised to other dimensions by identifying the quaternions as the even part Cℓ+3,0(R) of the Clifford algebra Cℓ3,0(R). This is an associative multivector algebra built up from fundamental basis elements σ1, σ2, σ3 using the product rules
If these fundamental basis elements are taken to represent vectors in 3D space, then it turns out that the reflection of a vector r in a plane perpendicular to a unit vector w can be written:
Two reflections make a rotation by an angle twice the angle between the two reflection planes, so
corresponds to a rotation of 180° in the plane containing σ1 and σ2.
This is very similar to the corresponding quaternion formula,
In fact, the two are identical, if we make the identification
and it is straightforward to confirm that this preserves the Hamilton relations
In this picture, quaternions correspond not to vectors but to bivectors – quantities with magnitude and orientations associated with particular 2D planes rather than 1D directions. The relation to complex numbers becomes clearer, too: in 2D, with two vector directions σ1 and σ2, there is only one bivector basis element σ1σ2, so only one imaginary. But in 3D, with three vector directions, there are three bivector basis elements σ1σ2, σ2σ3, σ3σ1, so three imaginaries.
This reasoning extends further.
In the Clifford algebra Cℓ4,0(R), there are six bivector basis elements, since with four different basic vector directions, six different pairs and therefore six different linearly independent planes can be defined. Rotations in such spaces using these generalisations of quaternions, called rotors, can be very useful for applications involving homogeneous coordinates. But it is only in 3D that the number of basis bivectors equals the number of basis vectors, and each bivector can be identified as a pseudovector.
There are several advantages for placing quaternions in this wider setting:[40]
Rotors are a natural part of geometric algebra and easily understood as the encoding of a double reflection.
In geometric algebra, a rotor and the objects it acts on live in the same space.
This eliminates the need to change representations and to encode new data structures and methods, which is traditionally required when augmenting linear algebra with quaternions.
Rotors are universally applicable to any element of the algebra, not just vectors and other quaternions, but also lines, planes, circles, spheres, rays, and so on.
In the conformal model of Euclidean geometry, rotors allow the encoding of rotation, translation and scaling in a single element of the algebra, universally acting on any element. In particular, this means that rotors can represent rotations around an arbitrary axis, whereas quaternions are limited to an axis through the origin.
Rotor-encoded transformations make interpolation particularly straightforward.
For further detail about the geometrical uses of Clifford algebras, see Geometric algebra.
Brauer group
The quaternions are "essentially" the only (non-trivial) central simple algebra (CSA) over the real numbers, in the sense that every CSA over the reals is Brauer equivalent to either the reals or the quaternions. Explicitly, the Brauer group of the reals consists of two classes, represented by the reals and the quaternions, where the Brauer group is the set of all CSAs, up to equivalence relation of one CSA being a matrix ring over another. By the Artin–Wedderburn theorem (specifically, Wedderburn's part), CSAs are all matrix algebras over a division algebra, and thus the quaternions are the only non-trivial division algebra over the reals.
CSAs – rings over a field, which are simple algebras (have no non-trivial 2-sided ideals, just as with fields) whose center is exactly the field – are a noncommutative analog of extension fields, and are more restrictive than general ring extensions. The fact that the quaternions are the only non-trivial CSA over the reals (up to equivalence) may be compared with the fact that the complex numbers are the only non-trivial field extension of the reals.
Quotations
"I regard it as an inelegance, or imperfection, in quaternions, or rather in the state to which it has been hitherto unfolded, whenever it becomes or seems to become necessary to have recourse to x, y, z, etc." — William Rowan Hamilton [Quoted in a letter from Tait to Cayley].
"Time is said to have only one dimension, and space to have three dimensions.
[…] The mathematical quaternion partakes of both these elements; in technical language it may be said to be "time plus space", or "space plus time": and in this sense it has, or at least involves a reference to, four dimensions.
And how the One of Time, of Space the Three, Might in the Chain of Symbols girdled be." — William Rowan Hamilton [Quoted in R.P. Graves, Life of Sir William Rowan Hamilton].
"Quaternions came from Hamilton after his really good work had been done; and, though beautifully ingenious, have been an unmixed evil to those who have touched them in any way, including Clerk Maxwell." — W. Thompson, Lord Kelvin. (1892).
"I came later to see that, as far as the vector analysis I required was concerned, the quaternion was not only not required, but was a positive evil of no inconsiderable magnitude; and that by its avoidance the establishment of vector analysis was made quite simple and its working also simplified, and that it could be conveniently harmonised with ordinary Cartesian work."
— Oliver Heaviside. (1893). Electromagnetic Theory volume I, pp. 134–135. London: The Electrician Printing and Publishing Company.
"Neither matrices nor quaternions and ordinary vectors were banished from these ten [additional] chapters.
For, in spite of the uncontested power of the modern Tensor Calculus, those older mathematical languages continue, in my opinion, to offer conspicuous advantages in the restricted field of special relativity.
Moreover, in science as well as in every-day life, the mastery of more than one language is also precious, as it broadens our views, is conducive to criticism with regard to, and guards against hypostasy [weak-foundation] of, the matter expressed by words or mathematical symbols."
— Ludwik Silberstein. (1924). Notes on preparing the second edition of his Theory of Relativity.
"... quaternions appear to exude an air of nineteenth century decay, as a rather unsuccessful species in the struggle-for-life of mathematical ideas.
Mathematicians, admittedly, still keep a warm place in their hearts for the remarkable algebraic properties of quaternions but, alas, such enthusiasm means little to the harder-headed physical scientist."
— Simon L. Altmann.
(1986).
See also
3-sphere
Associative algebra
Biquaternion
Clifford algebra
Conversion between quaternions and Euler angles
Division algebra
Dual quaternion
Dual complex number
Euler angles
Exterior algebra
Geometric algebra
Hurwitz quaternion
Hurwitz quaternion order
Hyperbolic quaternion
Hypercomplex number
Lénárt sphere
Octonion
Pauli matrices
Quaternion group
Quaternion variable
Quaternionic matrix
Quaternionic polytope
Quaternionic projective space
Quaternions and spatial rotation
Rotation operator (vector space)
Rotations in 4-dimensional Euclidean space
Slerp
Split-quaternion
Tesseract