In category theory, a branch of mathematics, a monad (also triple, triad, standard construction and fundamental construction)^[1] is an endofunctor (a functor mapping a category to itself), together with two natural transformations required to fulfill certain coherence conditions. Monads are used in the theory of pairs of adjoint functors, and they generalize closure operators on partially ordered sets to arbitrary categories.

Introduction and definition

A monad is a certain type ofendofunctor. For example, ifandare a pair ofadjoint functors, withleft adjoint to, then the compositionis a monad. Ifandare inverse functors, the corresponding monad is theidentity functor. In general, adjunctions are notequivalences—they relate categories of different natures. The monad theory matters as part of the effort to capture what it is that adjunctions 'preserve'. The other half of the theory, of what can be learned likewise from consideration of, is discussed under the dual theory of comonads.

Formal definition

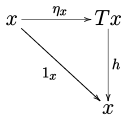
Throughout this articledenotes acategory. A monad onconsists of an endofunctortogether with twonatural transformations:(wheredenotes the identity functor on) and(whereis the functorfromto). These are required to fulfill the following conditions (sometimes calledcoherence conditions):

(as natural transformations );
(as natural transformations ; here denotes the identity transformation from to ).

We can rewrite these conditions using the following commutative diagrams:

See the article onnatural transformationsfor the explanation of the notationsand, or see below the commutative diagrams not using these notions:

The first axiom is akin to theassociativityinmonoidsif we think ofas the monoid's binary operation, and the second axiom is akin to the existence of anidentity element(which we think of as given by). Indeed, a monad oncan alternatively be defined as amonoidin the categorywhose objects are the endofunctors ofand whose morphisms are the natural transformations between them, with themonoidal structureinduced by the composition of endofunctors.

The power set monad

The power set monad is a monad on the category: For a setletbe thepower setofand for a functionletbe the function between the power sets induced by takingdirect imagesunder. For every set, we have a map, which assigns to everythesingleton. The function

takes a set of sets to its union. These data describe a monad.

Remarks

The axioms of a monad are formally similar to themonoidaxioms. In fact, monads are special cases of monoids, namely they are precisely the monoids amongendofunctors, which is equipped with the multiplication given by composition of endofunctors.

Comonads

Thecategorical dualdefinition is a formal definition of a comonad (or cotriple); this can be said quickly in the terms that a comonad for a categoryis a monad for theopposite category. It is therefore a functorfromto itself, with a set of axioms for counit and comultiplication that come from reversing the arrows everywhere in the definition just given.

Monads are to monoids as comonads are to comonoids. Every set is a comonoid in a unique way, so comonoids are less familiar in abstract algebra than monoids; however, comonoids in the category of vector spaces with its usual tensor product are important and widely studied under the name of coalgebras.

Terminological history

The notion of monad was invented by Roger Godement in 1958 under the name "standard construction." In the 1960s and 1970s, many people used the name "triple." The now standard term "monad" is due to Saunders Mac Lane.

Examples

Monads arising from adjunctions

Any adjunction

gives rise to a monad on C. This very widespread construction works as follows: the endofunctor is the composite

This endofunctor is quickly seen to be a monad, where the unit map stems from the unit mapof the adjunction, and the multiplication map is constructed using the counit map of the adjunction:

Double dualization

The double dualization monad, for a fixed field k arises from the adjunction

where both functors are given by sending avector spaceV to itsdual vector space. The associated monad sends a vector space V to itsdouble dual. This monad is discussed, in much greater generality, byKock (1970). Another instance of the same paradigm, discussed byRiehl (2017, Ex. 5.1.4), is the double power set monad, which is the monad on the category of sets, sending a set X to

where 2 denotes a 2-element set, andis thepower setof a set X.

Closure operators on partially ordered sets

For categories arising frompartially ordered sets(with a single morphism fromtoiff), then the formalism becomes much simpler: adjoint pairs areGalois connectionsand monads areclosure operators.

Free-forgetful adjunctions

For example, letbe theforgetful functorfromthe category Grpofgroupsto thecategory Setof sets, and letbe thefree groupfunctor from the category of sets to the category of groups. Thenis left adjoint of. In this case, the associated monadtakes a setand returns the underlying set of the free group

. The unit map of this monad is given by the maps

including any setinto the setin the natural way, as strings of length 1. Further, the multiplication of this monad is the map

made out of a natural concatenation or 'flattening' of 'strings of strings'. This amounts to two natural transformations. The preceding example about free groups can be generalized to any type of algebra in the sense of a variety of algebras in universal algebra. Thus, every such type of algebra gives rise to a monad on the category of sets. Importantly, the algebra type can be recovered from the monad (as the category of Eilenberg–Moore algebras), so monads can also be seen as generalizing varieties of universal algebras.

Another monad arising from an adjunction is whenis the endofunctor on the category of vector spaces which maps a vector spaceto itstensor algebra, and which maps linear maps to their tensor product. We then have a natural transformation corresponding to the embedding ofinto itstensor algebra, and a natural transformation corresponding to the map fromtoobtained by simply expanding all tensor products.

Codensity monads

Under mild conditions, functors not admitting a left adjoint also give rise to a monad, the so-called codensity monad. For example, the inclusion

does not admit a left adjoint. Its codensity monad is the monad on sets sending any set X to the set of ultrafilters on X. This monad is a submonad of the above-mentioned double power set monad. This and similar examples are discussed in Leinster (2013).

Algebras for a monad

Given a monadon a category, it is natural to consider *-algebras*, i.e., objects of C acted upon by T in a way which is compatible with the unit and multiplication of the monad. More formally, a T-algebrais an objectoftogether with an arrowofcalled the structure map of the algebra such that the diagrams


		and

commute.

A morphismof-algebras is an arrowofsuch that the diagram

commutes. T-algebras form a category called the *Eilenberg–Moore category and denoted by . For example, for the free group monad discussed above, a T-algebra is a set X together with a map from the free group generated by X towards X subject to associativity and unitality conditions. Such a structure is equivalent to saying that X is a group itself.

Another example is the distribution monad on the category of sets. It is defined by sending a set X to the set of functionswith finite support and so that. By inspection of the definitions, it can be shown that algebras over the distribution monad are equivalent toconvex sets, i.e., sets equipped with operationsforsubject to axioms resembling the behavior of convex linear combinationsin Euclidean space.^[2]

Monads and adjunctions

As was mentioned above, any adjunction gives rise to a monad. Conversely, every monad arises from some adjunction, namely the free-forgetful adjunction

whose left adjoint sends an object X to the free T-algebra T(X). However, there are usually several distinct adjunctions giving rise to a monad: letbe the category whose objects are the adjunctionssuch thatand whose arrows are the morphisms of adjunctions which are the identity on. Then the above free-forgetful adjunction involving the Eilenberg–Moore categoryis a terminal object in. An initial object is theKleisli category, which is by definition the full subcategory ofconsisting only of free T-algebras, i.e., T-algebras of the formfor some object x of C.

Monadic adjunctions

Given any adjunctionwith associated monad T, D can be factored as

i.e., G(Y) can be naturally endowed with a T-algebra structure for any Y in D. The adjunction is called a monadic adjunction if the first functoryields anequivalence of categoriesbetween D and the Eilenberg–Moore category.^[3] By extension, a functoris said to be monadic if it has a left adjointforming a monadic adjunction. For example, the free-forgetful adjunction between groups and sets is monadic, since algebras over the associated monad are groups, as was mentioned above. In general, knowing that an adjunction is monadic allows to reconstruct objects in D out of objects in C and the T-action.

Beck's monadicity theorem

Beck's monadicity theorem gives a necessary and sufficient condition for an adjunction to be monadic. A simplified version of this theorem states that G is monadic if it is conservative (or G reflects isomorphisms, i.e., a morphism in D is an isomorphism if and only if its image under G is an isomorphism in C) and C has and G preserves coequalizers.

For example, the forgetful functor from the category of compact Hausdorff spaces to sets is monadic. However the forgetful functor from all topological spaces to sets is not conservative since there are continuous bijective maps (between non-compact or non-Hausdorff spaces) which fail to be homeomorphisms. Thus, this forgetful functor is not monadic.^[4] The dual version of Beck's theorem, characterizing comonadic adjunctions, is relevant in different fields such as topos theory and topics in algebraic geometry related to descent. A first example of a comonadic adjunction is the adjunction

for a ring homomorphismbetween commutative rings. This adjunction is comonadic, by Beck's theorem, if and only if B isfaithfully flatas an A-module. It thus allows to descend B-modules, equipped with a descent datum (i.e., an action of the comonad given by the adjunction) to A-modules. The resulting theory offaithfully flat descentis widely applied in algebraic geometry.

Uses

Monads are used in functional programming to express types of sequential computation (sometimes with side-effects). See monads in functional programming, and the more mathematically oriented Wikibook module b:Haskell/Category theory.

In categorical logic, an analogy has been drawn between the monad-comonad theory, and modal logic via closure operators, interior algebras, and their relation to models of S4 and intuitionistic logics.

Generalization

It is possible to define monads in a2-category. Monads described above are monads for.

References

[1]

Citation Linkwww.tac.mta.caBarr, Michael; Wells, Charles (1985), "Toposes, Triples and Theories" (PDF), Grundlehren der mathematischen Wissenschaften, Springer-Verlag, 278, pp. 82 and 120, ISBN 0-387-96115-1.

Sep 30, 2019, 2:45 AM

[2]

Citation Link//doi.org/10.1007%2F978-3-642-15240-5_1Świrszcz, T., (1974), "Monadic functors and convexity", Bull. Acad. Polon. Sci. Sér. Sci. Math. Astronom. Phys., 22: 39–42, MR 0390019CS1 maint: extra punctuation (link), , doi:10.1007/978-3-642-15240-5_1 Missing or empty |title= (help)

Sep 30, 2019, 2:45 AM

[3]

Citation Linkopenlibrary.orgMacLane, Saunders (1978), Categories for the Working Mathematician, Graduate Texts in Mathematics, 5, doi:10.1007/978-1-4757-4721-8, ISBN 978-1-4419-3123-8 uses a stronger definition, where the two categories are isomorphic rather than equivalent.

Sep 30, 2019, 2:45 AM

[4]

Citation Linkopenlibrary.org, §§VI.3, VI.9)

Sep 30, 2019, 2:45 AM

[5]

Citation Linkwww.tac.mta.caCategory Theory for Computing Science

Sep 30, 2019, 2:45 AM

[6]

Citation Link//doi.org/10.7146%2Fmath.scand.a-1099510.7146/math.scand.a-10995

Sep 30, 2019, 2:45 AM

[7]

Citation Link//arxiv.org/abs/1209.36061209.3606