Green's theorem
Green's theorem
In mathematics, Green's theorem gives the relationship between a line integral around a simple closed curve C and a double integral over the plane region D bounded by C. It is named after George Green, though its first proof is due to Bernhard Riemann[1] and is the two-dimensional special case of the more general Kelvin–Stokes theorem.
Theorem
Let C be a positively oriented, piecewise smooth, simple closed curve in a plane, and let D be the region bounded by C. If L and M are functions of (x, y) defined on an open region containing D and having continuous partial derivatives there, then
In physics, Green's theorem finds many applications. One is solving two-dimensional flow integrals, stating that the sum of fluid outflowing from a volume is equal to the total outflow summed about an enclosing area. In plane geometry, and in particular, area surveying, Green's theorem can be used to determine the area and centroid of plane figures solely by integrating over the perimeter.
Proof when D is a simple region
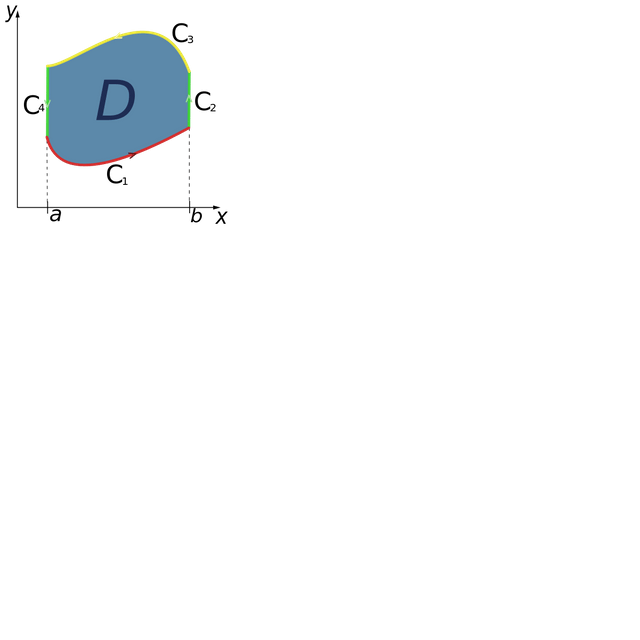
The following is a proof of half of the theorem for the simplified area D, a type I region where C1 and C3 are curves connected by vertical lines (possibly of zero length). A similar proof exists for the other half of the theorem when D is a type II region where C2 and C4 are curves connected by horizontal lines (again, possibly of zero length). Putting these two parts together, the theorem is thus proven for regions of type III (defined as regions which are both type I and type II). The general case can then be deduced from this special case by decomposing D into a set of type III regions.
If it can be shown that if
and
are true, then Green's theorem follows immediately for the region D. We can prove (1) easily for regions of type I, and (2) for regions of type II. Green's theorem then follows for regions of type III.
Assume region D is a type I region and can thus be characterized, as pictured on the right, by
where g1 and g2 are continuous functions on [a, b]. Compute the double integral in (1):
Now compute the line integral in (1). C can be rewritten as the union of four curves: C1, C2, C3, C4.
With C1, use the parametric equations: x = x, y = g1(x), a ≤ x ≤ b. Then
With C3, use the parametric equations: x = x, y = g2(x), a ≤ x ≤ b. Then
The integral over C3 is negated because it goes in the negative direction from b to a, as C is oriented positively (anticlockwise). On C2 and C4, x remains constant, meaning
Therefore,
Combining (3) with (4), we get (1) for regions of type I. A similar treatment yields (2) for regions of type II. Putting the two together, we get the result for regions of type III.
Proof for rectifiable Jordan curves
We are going to prove the following
We need the following lemmas:
- andarewhereis the oscillation ofon the range of.
Now we are in position to prove the Theorem:
- This yields
By Lemma 1(iii),
Combining these, we finally get
Validity under different hypotheses
The hypothesis of the last theorem are not the only ones under which Green's formula is true. Another common set of conditions is the following:
As a corollary of this, we get the Cauchy Integral Theorem for rectifiable Jordan curves:
the integral being a complex contour integral.
Now, analysing the sums used to define the complex contour integral in question, it is easy to realize that
the integrals on the RHS being usual line integrals. These remarks allow us to apply Green's Theorem to each one of these line integrals, finishing the proof.
Measure-theoretic assumptions
Green's formula also holds when, besides continuity assumptions,
Multiply-connected regions
![{\displaystyle {\begin{aligned}&\int _{\Gamma _{0}}p(x,y)\,dx+q(x,y)\,dy-\sum _{i=1}^{n}\int _{\Gamma _{i}}p(x,y)\,dx+q(x,y)\,dy\\[5pt]={}&\int _{D}\left\{{\frac {\partial q}{\partial e_{1}}}(x,y)-{\frac {\partial p}{\partial e_{2}}}(x,y)\right\}\,d(x,y).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b0a3feffd38b2ac095b5e5f36bedf83d12872aff)
Relationship to Stokes' theorem
The Kelvin–Stokes theorem:
The expression inside the integral becomes
![\nabla \times \mathbf {F} \cdot \mathbf {\hat {n}} =\left[\left({\frac {\partial 0}{\partial y}}-{\frac {\partial M}{\partial z}}\right)\mathbf {i} +\left({\frac {\partial L}{\partial z}}-{\frac {\partial 0}{\partial x}}\right)\mathbf {j} +\left({\frac {\partial M}{\partial x}}-{\frac {\partial L}{\partial y}}\right)\mathbf {k} \right]\cdot \mathbf {k} =\left({\frac {\partial M}{\partial x}}-{\frac {\partial L}{\partial y}}\right).](https://wikimedia.org/api/rest_v1/media/math/render/svg/77a90d83bc979c291f726a35cf8811cbf7706540)
Thus we get the right side of Green's theorem
Green's theorem is also a straightforward result of the general Stokes' theorem using differential forms and exterior derivatives:
![{\displaystyle {\begin{aligned}&\oint _{C}L\,dx+M\,dy=\oint _{\partial D}\omega =\int _{D}\,d\omega \\[5pt]={}&\int _{D}{\frac {\partial L}{\partial y}}\,dy\wedge \,dx+{\frac {\partial M}{\partial x}}\,dx\wedge \,dy=\iint _{D}\left({\frac {\partial M}{\partial x}}-{\frac {\partial L}{\partial y}}\right)\,dx\,dy.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad46c32ee065f2903c5f58ba6bfde6cf499c614f)
Relationship to the divergence theorem
Considering only two-dimensional vector fields, Green's theorem is equivalent to the two-dimensional version of the divergence theorem:
Start with the left side of Green's theorem:
Area calculation
See also
Planimeter
Method of image charges – A method used in electrostatics that takes advantage of the uniqueness theorem (derived from Green's theorem)
Shoelace formula – A special case of Green's theorem for simple polygons