Fermat's principle
Fermat's principle


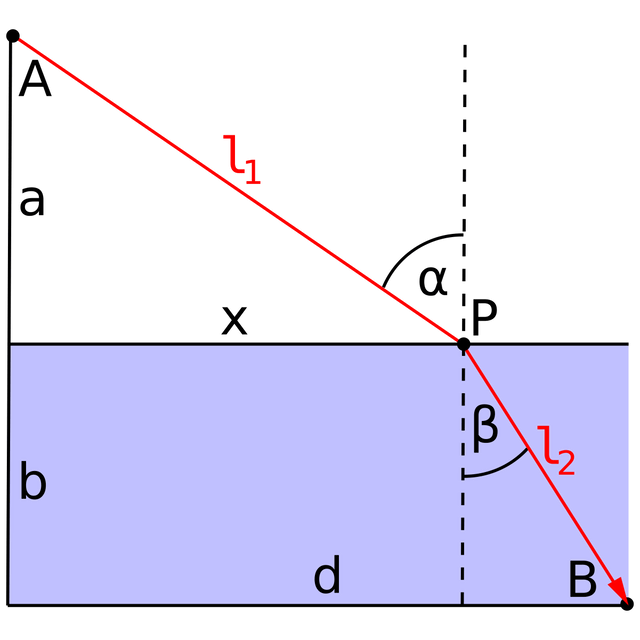
Fig. 2: Two points P and P′ on a path from A to B. For the purposes of Fermat's principle, the propagation time from P to P′ is taken as for a point-source at P, not (e.g.) for an arbitrary wavefront W passing through P. The surface Σ (with unit normal n̂ at P′) is the locus of points that a disturbance at P can reach in the same time that it takes to reach P′; in other words, Σ is the secondary wavefront with radius PP′.
Fermat's principle, also known as the principle of least time, is the link between ray optics and wave optics. In its original "strong" form,[9] Fermat's principle states that the path taken by a ray between two given points is the path that can be traversed in the least time. In order to be true in all cases, this statement must be weakened by replacing the "least" time with a time that is "stationary" with respect to variations of the path — so that a deviation in the path causes, at most, a second-order change in the traversal time. To put it loosely, a ray path is surrounded by close paths that can be traversed in very close times. It can be shown that this technical definition corresponds to more intuitive notions of a ray, such as a line of sight or the path of a narrow beam.
First proposed by the French mathematician Pierre de Fermat in 1662, as a means of explaining the ordinary law of refraction of light (Fig. 1), Fermat's principle was initially controversial because it seemed to ascribe knowledge and intent to nature. Not until the 19th century was it understood that nature's ability to test alternative paths is merely a fundamental property of waves.[10] Given points A and B, a wavefront expanding from A sweeps all possible ray paths radiating from A, whether they pass through B or not. If the wavefront reaches point B, it sweeps not only the ray path(s) from A to B, but also an infinitude of nearby paths with the same endpoints. Fermat's principle describes any ray that happens to reach point B; there is no implication that the ray "knew" the shortest path or "intended" to take that path.
For the purpose of comparing traversal times, the time from one point to the next nominated point is taken as if the first point were a point-source.[11] Without this condition, the traversal time would be ambiguous; for example, if the propagation time from P to P′ were reckoned from an arbitrary wavefront W containing P (Fig. 2), that time could be made arbitrarily small by suitably angling the wavefront.
Treating a point on the path as a source is the minimum requirement of Huygens' principle, and is part of the explanation of Fermat's principle. But it can also be shown that the geometric construction by which Huygens tried to apply his own principle (as distinct from the principle itself) is simply an invocation of Fermat's principle.[12] Hence all the conclusions that Huygens drew from that construction — including, without limitation, the laws of rectilinear propagation of light, ordinary reflection, ordinary refraction, and the extraordinary refraction of "Iceland crystal" (calcite) — are also consequences of Fermat's principle.
Derivation
Sufficient conditions
Let us suppose that:
- (1) A disturbance propagates sequentially through amedium(a vacuum or some material, not necessarily homogeneous orisotropic), withoutaction at a distance;
- (2) During propagation, the influence of the disturbance at any intermediate point P upon surrounding points has a non-zero angular spread (as if P were a source), so that a disturbance originating at any point A arrives at any other point B via an infinitude of paths, by which B receives an infinitude of delayed versions of the disturbance at A;[1] and
- (3) These delayed versions of the disturbance will reinforce each other at B if they are synchronized within some tolerance.
Then the various propagation paths from A to B will help each other if their traversal times agree within the said tolerance. For a small tolerance (in the limiting case), the permissible range of variations of the path is maximized if the path is such that its traversal time is stationary with respect to the variations, so that a variation of the path causes at most a second-order change in the traversal time.[13]
The most obvious example of a stationarity in traversal time is a (local or global) minimum — that is, a path of least time, as in the "strong" form of Fermat's principle. But that condition is not essential to the argument.[2]
Having established that a path of stationary traversal time is reinforced by a maximally wide corridor of neighboring paths, we still need to explain how this reinforcement corresponds to intuitive notions of a ray. But, for brevity in the explanations, let us first define a ray path as a path of stationary traversal time.
A ray as a signal path (line of sight)
If the corridor of paths reinforcing a ray path from A to B is substantially obstructed, this will significantly alter the disturbance reaching B from A — unlike a similar-sized obstruction outside any such corridor, blocking paths that do not reinforce each other. The former obstruction will significantly disrupt the signal reaching B from A, while the latter will not; thus the ray path marks a signal path. If the signal is visible light, the former obstruction will significantly affect the appearance of an object at A as seen by an observer at B, while the latter will not; so the ray path marks a line of sight.
In optical experiments, a line of sight is routinely assumed to be a ray path.[14]
A ray as an energy path (beam)

Fig. 3: An experiment demonstrating refraction (and partial reflection) of rays — approximated by, or contained in, narrow beams.
If the corridor of paths reinforcing a ray path from A to B is substantially obstructed, this will significantly affect the energy reaching B from A — unlike a similar-sized obstruction outside any such corridor. Thus the ray path marks an energy path — as does a beam.
Suppose that a wavefront expanding from point A passes point P, which lies on a ray path from point A to point B. By definition, all points on the wavefront have the same propagation time from A. Now let the wavefront be blocked except for a window, centered on P, and small enough to lie within the corridor of paths that reinforce the ray path from A to B. Then all points on the unobstructed portion of the wavefront will have, nearly enough, equal propagation times to B, but not to points in other directions, so that B will be in the direction of peak intensity of the beam admitted through the window.[15] So the ray path marks the beam. And in optical experiments, a beam is routinely considered as a collection of rays or (if it is narrow) as an approximation to a ray (Fig. 3).[16]
Analogies
According to the "strong" form of Fermat's principle, the problem of finding the path of a light ray from point A in a medium of faster propagation, to point B in a medium of slower propagation, is analogous to the problem faced by a lifeguard in deciding where to enter the water in order to reach a drowning swimmer as soon as possible, given that the lifeguard can run faster than (s)he can swim.[17] But that analogy falls short of explaining the behavior of the light, because the lifeguard can think about the problem (even if only for an instant) whereas the light presumably cannot. The discovery that ants are capable of similar calculations[18] does not bridge the gap between the animate and the inanimate.
In contrast, the above assumptions (1) to (3) hold for any wavelike disturbance and explain Fermat's principle in purely mechanistic terms, without any imputation of knowledge or purpose.
The principle applies to waves in general, including (e.g.) sound waves in fluids and elastic waves in solids.[19] In a modified form, it even works for matter waves: in quantum mechanics, the classical path of a particle is obtainable by applying Fermat's principle to the associated wave — except that, because the frequency may vary with the path, the stationarity is in the phase shift (or number of cycles) and not necessarily in the time.[20][21]
Fermat's principle is most familiar, however, in the case of visible light: it is the link between geometrical optics, which describes certain optical phenomena in terms of rays, and the wave theory of light, which explains the same phenomena on the hypothesis that light consists of waves.

Fig. 4: Two iterations of Huygens' construction. In the first iteration, the later wavefront W′ is derived from the earlier wavefront W by taking the envelope of all the secondary wavefronts (gray arcs) expanding in a given time from all the points (e.g., P) on W. The arrows show the ray directions.
In this article we distinguish between Huygens' principle, which states that every point crossed by a traveling wave becomes the source of a secondary wave, and Huygens' construction, which is described below.
Let the surface W be a wavefront at time t, and let the surface W′ be the same wavefront at the later time t + Δt (Fig. 4). Then, according to Huygens construction,[22]
- (a) W′is the *envelope
- (common tangent surface), on the forward side of
The construction may be repeated in order to find successive positions of the primary wavefront, and successive points on the ray.
The ray direction given by this construction is the radial direction of the secondary wavefront,[23] and may differ from the normal of the secondary wavefront (cf. Fig. 2), and therefore from the normal of the primary wavefront at the point of tangency. Hence the ray velocity, in magnitude and direction, is the radial velocity of an infinitesimal secondary wavefront, and is generally a function of location and direction.[24]
From the construction it follows that
- (i) the time taken for a secondary wavefront fromPto reach another pointQ′onW′is stationary with respect to the displacementP′Q′, and(ii) the time taken for a secondary wavefront to reachP′from another pointQonWis stationary with respect to the displacementPQ.
So Huygens' construction implicitly defines a ray path as a path of stationary traversal time between successive positions of a wavefront, the time being reckoned from a point-source on the earlier wavefront.[3] This conclusion remains valid if the secondary wavefronts are reflected or refracted by surfaces of discontinuity in the properties of the medium, provided that the comparison is restricted to the affect paths and the affected portions of the wavefronts.[4]
Fermat's principle, however, is conventionally expressed in point-to-point terms, not wavefront-to-wavefront terms. Accordingly, let us modify the example by supposing that the wavefront which becomes surface W at time t, and which becomes surface W′ at the later time t + Δt, is emitted from point A at time 0. Let P be a point on W (as before), and B a point on W′. And let A,W, W′, and B be given, so that the problem is to find P.
If P satisfies Huygens' construction, so that the secondary wavefront from P is tangential to W′ at B, then PB is a path of stationary traversal time from W to B. Adding the fixed time from A to W, we find that APB is the path of stationary traversal time from A to B (possibly with a restricted domain of comparison, as noted above), in accordance with Fermat's principle. The argument works just as well in the converse direction. Thus Huygens' construction and Fermat's principle are geometrically equivalent.[27][5]
Through this equivalence, Fermat's principle sustains Huygens' construction and thence all the conclusions that Huygens was able to draw from that construction. In short, "The laws of geometrical optics may be derived from Fermat's principle".[28] With the exception of the Fermat-Huygens principle itself, these laws are special cases in the sense that they depend on further assumptions about the media. Two of them are mentioned under the next heading.
Special cases
Isotropic media: Rays normal to wavefronts
In an isotropic medium, because the propagation speed is independent of direction, the secondary wavefronts that expand from points on a primary wavefront in a given infinitesimal time are spherical,[29] so that their radii are normal to their common tangent surface at the points of tangency. But their radii mark the ray directions, and their common tangent surface is a general wavefront. Thus the rays are normal (orthogonal) to the wavefronts.[30]
Because much of the teaching of optics concentrates on isotropic media, treating anisotropic media as an optional topic, the assumption that the rays are normal to the wavefronts can become so pervasive that even Fermat's principle is explained under that assumption,[31] although in fact Fermat's principle is more general.
Homogeneous media: Rectilinear propagation
In a homogeneous medium (also called a uniform medium), all the secondary wavefronts that expand from a given primary wavefront W in a given time Δt are congruent and similarly oriented, so that their envelope W′ may be considered as the envelope of a single secondary wavefront which preserves its orientation while its center (source) moves over W. If P is its center while P′ is its point of tangency with W′, then P′ moves parallel to P, so that the plane tangential to W′ at P′ is parallel to the plane tangential to W at P. Let another (congruent and similarly orientated) secondary wavefront be centered on P′, moving with P, and let it meet its envelope W″ at point P″. Then, by the same reasoning, the plane tangential to W″ at P″ is parallel to the other two planes. Hence, due to the congruence and similar orientations, the ray directions PP′ and P′P″ are the same (but not necessarily normal to the wavefronts, since the secondary wavefronts are not necessarily spherical). This construction can be repeated any number of times, giving a straight ray of any length. Thus a homogeneous medium admits rectilinear rays.[32]
Modern version
Formulation in terms of refractive index
 (that is, at the radial speed of the local secondary wavefront, for each location and direction on the path). Then the traversal time of the entire pathΓis
(that is, at the radial speed of the local secondary wavefront, for each location and direction on the path). Then the traversal time of the entire pathΓis | (1) |
(where A and B simply denote the endpoints and are not to be construed as values of t or s). The condition for Γ to be a ray path is that the first-order change in T due to a change in Γ is zero; that is,
 .
.Now let us define the optical length of a given path (optical path length, OPL) as the distance traversed by a ray in a homogeneous isotropic reference medium (e.g., a vacuum) in the same time that it takes to traverse the given path at the local ray velocity.[33] Then, if c denotes the propagation speed in the reference medium (e.g., the speed of light in a vacuum), the optical length of a path traversed in time dt is dS = c dt, and the optical length of a path traversed in time T is S = cT. So, multiplying equation (1) through by c , we obtain

 is the ray index — that is, therefractive indexcalculated on the ray velocity instead of the usualphase velocity(wave-normal velocity).[34] For an infinitesimal path, we have
is the ray index — that is, therefractive indexcalculated on the ray velocity instead of the usualphase velocity(wave-normal velocity).[34] For an infinitesimal path, we have indicating that the optical length is the physical length multiplied by the ray index: the OPL is a notional geometric quantity, from which time has been factored out. In terms of OPL, the condition forΓto be a ray path (Fermat's principle) becomes
indicating that the optical length is the physical length multiplied by the ray index: the OPL is a notional geometric quantity, from which time has been factored out. In terms of OPL, the condition forΓto be a ray path (Fermat's principle) becomes . . | (2) |
This has the form of Maupertuis's principle in classical mechanics (for a single particle), with the ray index in optics taking the role of momentum or velocity in mechanics.[35]
Relation to Hamilton's principle
If x,y,z are Cartesian coordinates and an overdot denotes differentiation with respect to s , Fermat's principle (2) may be written[38]

In the case of an isotropic medium, we may replace nr with the normal refractive index n(x,y,z), which is simply a scalar field. If we then define the optical Lagrangian[39] as

Fermat's principle becomes[40]
 .
.If the direction of propagation is always such that we can use z instead of s as the parameter of the path (and the overdot to denote differentiation w.r.t. z instead of s), the optical Lagrangian can instead be written[41]

so that Fermat's principle becomes
 .
.This has the form of Hamilton's principle in classical mechanics, except that the time dimension is missing: the third spatial coordinate in optics takes the role of time in mechanics.[42] The optical Lagrangian is the function which, when integrated w.r.t. the parameter of the path, yields the OPL; it is the foundation of Lagrangian and Hamiltonian optics.[43]
History
Fermat vs. the Cartesians

Pierre de Fermat (1607[44] –1665).
If a ray follows a straight line, it obviously takes the path of least length. Hero of Alexandria, in his Catoptrics (1st century CE), showed that the ordinary law of reflection off a plane surface follows from the premise that the total length of the ray path is a minimum.[45] In 1657, Pierre de Fermat received from Marin Cureau de la Chambre a copy of newly published treatise, in which La Chambre noted Hero's principle and complained that it did not work for refraction.[46]
Fermat replied that refraction might be brought into the same framework by supposing that light took the path of least resistance, and that different media offered different resistances. His eventual solution, described in a letter to La Chambre dated 1 January 1662, construed "resistance" as inversely proportional to speed, so that light took the path of least time. That premise yielded the ordinary law of refraction, provided that light traveled more slowly in the optically denser medium.[47][7]
Fermat's solution was a landmark in that it unified the then-known laws of geometrical optics under a variational principle or action principle, setting the precedent for the principle of least action in classical mechanics and the corresponding principles in other fields (see History of variational principles in physics).[48] It was the more notable because it used the method of adequality, which may be understood in retrospect as finding the point where the slope of an infinitesimally short chord is zero,[49] without the intermediate step of finding a general expression for the slope (the derivative).
It was also immediately controversial. The ordinary law of refraction was at that time attributed to René Descartes (d. 1650), who had tried to explain it by supposing that light was a force that propagated instantaneously, or that light was analogous to a tennis ball that traveled faster in the denser medium,[50][51] either premise being inconsistent with Fermat's. Descartes' most prominent defender, Claude Clerselier, criticized Fermat for apparently ascribing knowledge and intent to nature, and for failing to explain why nature should prefer to economize on time rather than distance. Clerselier wrote in part:
- The principle that you take as the basis of your demonstration, namely that nature always acts in the shortest and simplest ways, is merely a moral principle and not a physical one; it is not, and cannot be, the cause of any effect in nature.... For otherwise we would attribute knowledge to nature; but here, by "nature", we understand only this order and this law established in the world as it is, which acts without foresight, without choice, and by a necessary determination.
- This same principle would make nature irresolute... For I ask you... when a ray of light must pass from a point in a rare medium to a point in a dense one, is there not reason for nature to hesitate if, by your principle, it must choose the straight line as soon as the bent one, since if the latter proves shorter in time, the former is shorter and simpler in length? Who will decide and who will pronounce? [52]
Fermat, being unaware of the mechanistic foundations of his own principle, was not well placed to defend it, except as a purely geometric and kinematic proposition.[53][54] The wave theory of light, first proposed by Robert Hooke in the year of Fermat's death,[55] and rapidly improved by Ignace-Gaston Pardies[56] and (especially) Christiaan Huygens,[57] contained the necessary foundations; but the recognition of this fact was surprisingly slow.
Huygens' oversight

Christiaan Huygens (1629–1695).
Huygens repeatedly referred to the envelope of his secondary wavefronts as the termination of the movement,[58] meaning that the later wavefront was the outer boundary that the disturbance could reach in a given time,[59] which was therefore the minimum time in which each point on the later wavefront could be reached. But he did not argue that the direction of minimum time was that from the secondary source to the point of tangency; instead, he deduced the ray direction from the extent of the common tangent surface corresponding to a given extent of the initial wavefront.[60] His only endorsement of Fermat's principle was limited in scope: having derived the law of ordinary refraction, for which the rays are normal to the wavefronts,[61] Huygens gave a geometric proof that a ray refracted according to this law takes the path of least time.[62] He would hardly have thought this necessary if he had known that the principle of least time followed directly from the same common-tangent construction by which he had deduced not only the law of ordinary refraction, but also the laws of rectilinear propagation and ordinary reflection (which were also known to follow from Fermat's principle), and a previously unknown law of extraordinary refraction — the last by means of secondary wavefronts that were spheroidal rather than spherical, with the result that the rays were generally oblique to the wavefronts. It was as if Huygens had not noticed that his construction implied Fermat's principle, and even as if he thought he had found an exception to that principle. Manuscript evidence cited by Alan E. Shapiro tends to confirm that Huygens believed the principle of least time to be invalid "in double refraction, where the rays are not normal to the wave fronts".[63]
Shapiro further reports that the only three authorities who accepted "Huygens' principle" in the 17th and 18th centuries, namely Philippe de La Hire, Denis Papin, and Gottfried Wilhelm Leibniz, did so because it accounted for the extraordinary refraction of "Iceland crystal" (calcite) in the same manner as the previously known laws of geometrical optics.[64] One can only speculate on how differently Huygens' theory might have been received if it had overtly subsumed and extended Fermat's principle.
Laplace, Young, Fresnel, and Lorentz

Pierre-Simon Laplace (1749–1827).

Thomas Young (1773–1829).

Augustin-Jean Fresnel (1788–1827).
On 30 January 1809,[65] Pierre-Simon Laplace, reporting on the work of his protégé Étienne-Louis Malus, claimed that the extraordinary refraction of calcite could be explained under the corpuscular theory of light with the aid of Maupertuis's principle of least action: that the integral of speed with respect to distance was a minimum. The corpuscular speed that satisfied this principle was proportional to the reciprocal of the ray speed given by the radius of Huygens' spheroid. Laplace continued:
According to Huygens, the velocity of the extraordinary ray, in the crystal, is simply expressed by the radius of the spheroid; consequently his hypothesis does not agree with the principle of the least action: but it is remarkable that it agrees with the principle of Fermat, which is, that light passes, from a given point without the crystal, to a given point within it, in the least possible time; for it is easy to see that this principle coincides with that of the least action, if we invert the expression of the velocity.[66]
Laplace's report was the subject of a wide-ranging rebuttal by Thomas Young, who wrote in part:
The principle of Fermat, although it was assumed by that mathematician on hypothetical, or even imaginary grounds, is in fact a fundamental law with respect to undulatory motion, and is explicitly [sic] the basis of every determination in the Huygenian theory... Mr. Laplace seems to be unacquainted with this most essential principle of one of the two theories which he compares; for he says, that "it is remarkable," that the Huygenian law of extraordinary refraction agrees with the principle of Fermat; which he would scarcely have observed, if he had been aware that the law was an immediate consequence of the principle.[67]
In fact Laplace was aware that Fermat's principle follows from Huygens' construction in the case of refraction from an isotropic medium to an anisotropic one; a geometric proof was contained in the long version of Laplace's report, printed in 1810.[68]
Young's claim was more general than Laplace's, and likewise upheld Fermat's principle even in the case of extraordinary refraction, in which the rays are generally not perpendicular to the wavefronts. Unfortunately, however, the omitted middle sentence of the quoted paragraph by Young began "The motion of every undulation must necessarily be in a direction perpendicular to its surface..." (emphasis added), and was therefore bound to sow confusion rather than clarity.
No such confusion subsists in Augustin-Jean Fresnel's "Second Memoir" on double refraction (Fresnel, 1827), which addresses Fermat's principle in several places (without naming Fermat), proceeding from the special case in which rays are normal to wavefronts, to the general case in which rays are paths of least time or stationary time. (In the following summary, page numbers refer to Alfred W. Hobson's translation.)
For refraction of a plane wave at parallel incidence on one face of an anisotropic crystalline wedge (pp. 291–2), in order to find the "first ray arrived" at an observation point beyond the other face of the wedge, it suffices to treat the rays outside the crystal as normal to the wavefronts, and within the crystal to consider only the parallel wavefronts (whatever the ray direction). So in this case, Fresnel does not attempt to trace the complete ray path.[8]
Next, Fresnel considers a ray refracted from a point-source M inside a crystal, through a point A on the surface, to an observation point B outside (pp. 294–6). The surface passing through B and given by the "locus of the disturbances which arrive first" is, according to Huygens' construction, normal to "the ray AB of swiftest arrival". But this construction requires knowledge of the "surface of the wave" (that is, the secondary wavefront) within the crystal.
Then he considers a plane wavefront propagating in a medium with non-spherical secondary wavefronts, oriented so that the ray path given by Huygens' construction — from the source of the secondary wavefront to its point of tangency with the subsequent primary wavefront — is not normal to the primary wavefronts (p. 296). He shows that this path is nevertheless "the path of quickest arrival of the disturbance" from the earlier primary wavefront to the point of tangency.
In a later heading (p. 305) he declares that "The construction of Huygens, which determines the path of swiftest arrival," is applicable to secondary wavefronts of any shape. He then notes that when we apply Huygens' construction to refraction into a crystal with a two-sheeted secondary wavefront, and draw the lines from the two points of tangency to the center of the secondary wavefront, "we shall have the directions of the two paths of swiftest arrival, and consequently of the ordinary and of the extraordinary ray."
Under the heading "Definition of the word Ray" (p. 309), he concludes that this term must be applied to the line which joins the center of the secondary wave to a point on its surface, whatever the inclination of this line to the surface.
As a "new consideration" (pp. 310–11), he notes that if a plane wavefront is passed through a small hole centered on point E, then the direction ED of maximum intensity of the resulting beam will be that in which the secondary wave starting from E will "arrive there the first", and the secondary wavefronts from opposite sides of the hole (equidistant from E) will "arrive at D in the same time" as each other. This direction is not assumed to be normal to any wavefront.
Thus Fresnel showed, even for anisotropic media, that the ray path given by Huygens' construction is the path of least time between successive positions of a plane or diverging wavefront, that the ray velocities are the radii of the secondary "wave surface" after unit time, and that a stationary traversal time accounts for the direction of maximum intensity of a beam. However, establishing the general equivalence between Huygens' construction and Fermat's principle would have required further consideration of Fermat's principle in point-to-point terms.
According to Adriaan J. de Witte (1959), the equivalence of Huygens' construction and Fermat's principle was discussed by Hendrik Lorentz in 1907.[69] De Witte offers his own proof, which "although in essence the same, is believed to be more cogent and more general." But, he notes, "The matter seems to have escaped treatment in textbooks."[70]
See also
Action (physics)
Adequality
Augustin-Jean Fresnel
Eikonal equation
Fermat’s and energy variation principles in field theory
Huygens' principle
Path integral formulation
Pierre de Fermat
Principle of least action
Snell's law
Thomas Young (scientist)