Everipedia Logo
Everipedia is now IQ.wiki - Join the IQ Brainlist and our Discord for early access to editing on the new platform and to participate in the beta testing.
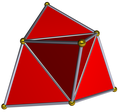
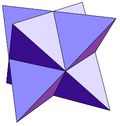
Deltahedron

Deltahedron

In geometry, a deltahedron (plural deltahedra) is a polyhedron whose faces are all equilateral triangles. The name is taken from the Greek majuscule delta (Δ), which has the shape of an equilateral triangle. There are infinitely many deltahedra, but of these only eight are convex, having 4, 6, 8, 10, 12, 14, 16 and 20 faces.[1] The number of faces, edges, and vertices is listed below for each of the eight convex deltahedra.

The eight convex deltahedra

There are only eight strictly-convex deltahedra: three are regular polyhedra, and five are Johnson solids.

Regular deltahedra
ImageNameFacesEdgesVerticesVertex configurationsSymmetry group
Tetrahedron.jpgtetrahedron4644 × 33Td, [3,3]
Octahedron.svgoctahedron81266 × 34Oh, [4,3]
Icosahedron.jpgicosahedron20301212 × 35Ih, [5,3]
Johnson deltahedra
ImageNameFacesEdgesVerticesVertex configurationsSymmetry group
Triangular dipyramid.pngtriangular bipyramid6952 × 33
3 × 34		D3h, [3,2]
Pentagonal dipyramid.pngpentagonal bipyramid101575 × 34
2 × 35		D5h, [5,2]
Snub disphenoid.pngsnub disphenoid121884 × 34
4 × 35		D2d, [2,2]
Triaugmented triangular prism.pngtriaugmented triangular prism142193 × 34
6 × 35		D3h, [3,2]
Gyroelongated square dipyramid.pnggyroelongated square bipyramid1624102 × 34
8 × 35		D4d, [4,2]

In the 6-faced deltahedron, some vertices have degree 3 and some degree 4. In the 10-, 12-, 14-, and 16-faced deltahedra, some vertices have degree 4 and some degree 5. These five irregular deltahedra belong to the class of Johnson solids: convex polyhedra with regular polygons for faces.

Deltahedra retain their shape even if the edges are free to rotate around their vertices so that the angles between edges are fluid. Not all polyhedra have this property: for example, if you relax some of the angles of a cube, the cube can be deformed into a non-right square prism.

There is no 18-faced convex deltahedron.[2] However, the edge-contracted icosahedron gives an example of an octadecahedron that can either be made convex with 18 irregular triangular faces, or made with equilateral triangles that include two coplanar sets of three triangles.

Non-strictly-convex cases

There are infinitely many cases with coplanar triangles, allowing for sections of the infinite triangular tilings. If the sets of coplanar triangles are considered a single face, a smaller set of faces, edges, and vertices can be counted. The coplanar triangular faces can be merged into rhombic, trapezoidal, hexagonal, or other equilateral polygon faces. Each face must be a convex polyiamond such as [[INLINE_IMAGE|//upload.wikimedia.org/wikipedia/commons/thumb/6/66/Polyiamond-1-1.svg/20px-Polyiamond-1-1.svg.png|//upload.wikimedia.org/wikipedia/commons/thumb/6/66/Polyiamond-1-1.svg/30px-Polyiamond-1-1.svg.png 1.5x, //upload.wikimedia.org/wikipedia/commons/thumb/6/66/Polyiamond-1-1.svg/40px-Polyiamond-1-1.svg.png 2x|Polyiamond-1-1.svg|h18|w20]], [[INLINE_IMAGE|//upload.wikimedia.org/wikipedia/commons/thumb/1/17/Polyiamond-2-1.svg/30px-Polyiamond-2-1.svg.png|//upload.wikimedia.org/wikipedia/commons/thumb/1/17/Polyiamond-2-1.svg/45px-Polyiamond-2-1.svg.png 1.5x, //upload.wikimedia.org/wikipedia/commons/thumb/1/17/Polyiamond-2-1.svg/60px-Polyiamond-2-1.svg.png 2x|Polyiamond-2-1.svg|h19|w30]], [[INLINE_IMAGE|//upload.wikimedia.org/wikipedia/commons/thumb/9/92/Polyiamond-3-1.svg/30px-Polyiamond-3-1.svg.png|//upload.wikimedia.org/wikipedia/commons/thumb/9/92/Polyiamond-3-1.svg/45px-Polyiamond-3-1.svg.png 1.5x, //upload.wikimedia.org/wikipedia/commons/thumb/9/92/Polyiamond-3-1.svg/60px-Polyiamond-3-1.svg.png 2x|Polyiamond-3-1.svg|h15|w30]], [[INLINE_IMAGE|//upload.wikimedia.org/wikipedia/commons/thumb/d/d5/Polyiamond-4-2.svg/40px-Polyiamond-4-2.svg.png|//upload.wikimedia.org/wikipedia/commons/thumb/d/d5/Polyiamond-4-2.svg/60px-Polyiamond-4-2.svg.png 1.5x, //upload.wikimedia.org/wikipedia/commons/thumb/d/d5/Polyiamond-4-2.svg/80px-Polyiamond-4-2.svg.png 2x|Polyiamond-4-2.svg|h16|w40]], [[INLINE_IMAGE|//upload.wikimedia.org/wikipedia/commons/thumb/c/ce/Polyiamond-4-3.svg/30px-Polyiamond-4-3.svg.png|//upload.wikimedia.org/wikipedia/commons/thumb/c/ce/Polyiamond-4-3.svg/45px-Polyiamond-4-3.svg.png 1.5x, //upload.wikimedia.org/wikipedia/commons/thumb/c/ce/Polyiamond-4-3.svg/60px-Polyiamond-4-3.svg.png 2x|Polyiamond-4-3.svg|h27|w30]], [[INLINE_IMAGE|//upload.wikimedia.org/wikipedia/commons/thumb/5/56/Polyiamond-5-1.svg/50px-Polyiamond-5-1.svg.png|//upload.wikimedia.org/wikipedia/commons/thumb/5/56/Polyiamond-5-1.svg/75px-Polyiamond-5-1.svg.png 1.5x, //upload.wikimedia.org/wikipedia/commons/thumb/5/56/Polyiamond-5-1.svg/100px-Polyiamond-5-1.svg.png 2x|Polyiamond-5-1.svg|h17|w50]], [[INLINE_IMAGE|//upload.wikimedia.org/wikipedia/commons/thumb/3/35/Polyiamond-6-1.svg/60px-Polyiamond-6-1.svg.png|//upload.wikimedia.org/wikipedia/commons/thumb/3/35/Polyiamond-6-1.svg/90px-Polyiamond-6-1.svg.png 1.5x, //upload.wikimedia.org/wikipedia/commons/thumb/3/35/Polyiamond-6-1.svg/120px-Polyiamond-6-1.svg.png 2x|Polyiamond-6-1.svg|h18|w60]] and [[INLINE_IMAGE|//upload.wikimedia.org/wikipedia/commons/thumb/1/17/Polyiamond-6-11.svg/30px-Polyiamond-6-11.svg.png|//upload.wikimedia.org/wikipedia/commons/thumb/1/17/Polyiamond-6-11.svg/45px-Polyiamond-6-11.svg.png 1.5x, //upload.wikimedia.org/wikipedia/commons/thumb/1/17/Polyiamond-6-11.svg/60px-Polyiamond-6-11.svg.png 2x|Polyiamond-6-11.svg|h27|w30]], ...[3]

Some smaller examples include:

Coplanar deltahedra
ImageNameFacesEdgesVerticesVertex configurationsSymmetry group
Augmented octahedron.pngAugmented octahedron
Augmentation
1 tet + 1 oct		10Polyiamond-1-1.svg1571 × 33
3 × 34
3 × 35
0 × 36		C3v, [3]
4Polyiamond-1-1.svg
3Polyiamond-2-1.svg		12
Gyroelongated triangular bipyramid.pngTrigonal trapezohedron
Augmentation
2 tets + 1 oct		12Polyiamond-1-1.svg1882 × 33
0 × 34
6 × 35
0 × 36		C3v, [3]
6Polyiamond-2-1.svg12
Tet2Oct solid.pngAugmentation
2 tets + 1 oct		12Polyiamond-1-1.svg1882 × 33
1 × 34
4 × 35
1 × 36		C2v, [2]
2Polyiamond-1-1.svg
2Polyiamond-2-1.svg
2Polyiamond-3-1.svg		117
Triangulated monorectified tetrahedron.pngTriangular frustum
Augmentation
3 tets + 1 oct		14Polyiamond-1-1.svg2193 × 33
0 × 34
3 × 35
3 × 36		C3v, [3]
1Polyiamond-1-1.svg
3Polyiamond-3-1.svg
1Polyiamond-4-3.svg		96
TetOct2 solid2.pngElongated octahedron
Augmentation
2 tets + 2 octs		16Polyiamond-1-1.svg24100 × 33
4 × 34
4 × 35
2 × 36		D2h, [2,2]
4Polyiamond-1-1.svg
4Polyiamond-3-1.svg		126
Triangulated tetrahedron.pngTetrahedron
Augmentation
4 tets + 1 oct		16Polyiamond-1-1.svg24104 × 33
0 × 34
0 × 35
6 × 36		Td, [3,3]
4Polyiamond-4-3.svg64
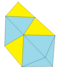Tet3Oct2 solid.pngAugmentation
3 tets + 2 octs		18Polyiamond-1-1.svg27111 × 33
2 × 34
5 × 35
3 × 36		D2h, [2,2]
2Polyiamond-1-1.svg
1Polyiamond-2-1.svg
2Polyiamond-3-1.svg
2Polyiamond-4-2.svg		149
Double diminished icosahedron.pngEdge-contracted icosahedron18Polyiamond-1-1.svg27110 × 33
2 × 34
8 × 35
1 × 36		C2v, [2]
12Polyiamond-1-1.svg
2Polyiamond-3-1.svg		2210
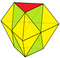Triangulated truncated triangular bipyramid.pngTriangular bifrustum
Augmentation
6 tets + 2 octs		20Polyiamond-1-1.svg30120 × 33
3 × 34
6 × 35
3 × 36		D3h, [3,2]
2Polyiamond-1-1.svg
6Polyiamond-3-1.svg		159
Augmented triangular cupola.pngtriangular cupola
Augmentation
4 tets + 3 octs		22Polyiamond-1-1.svg33130 × 33
3 × 34
6 × 35
4 × 36		C3v, [3]
3Polyiamond-1-1.svg
3Polyiamond-3-1.svg
1Polyiamond-4-3.svg
1Polyiamond-6-11.svg		159
Triangulated bipyramid.pngTriangular bipyramid
Augmentation
8 tets + 2 octs		24Polyiamond-1-1.svg36142 × 33
3 × 34
0 × 35
9 × 36		D3h, [3]
6Polyiamond-4-3.svg95
Augmented hexagonal antiprism flat.pngHexagonal antiprism24Polyiamond-1-1.svg36140 × 33
0 × 34
12 × 35
2 × 36		D6d, [12,2
]
12Polyiamond-1-1.svg
2Polyiamond-6-11.svg		2412
Triangulated truncated tetrahedron.pngTruncated tetrahedron
Augmentation
6 tets + 4 octs		28Polyiamond-1-1.svg42160 × 33
0 × 34
12 × 35
4 × 36		Td, [3,3]
4Polyiamond-1-1.svg
4Polyiamond-6-11.svg		1812
Triangulated octahedgon.pngTetrakis cuboctahedron
Octahedron
Augmentation
8 tets + 6 octs		32Polyiamond-1-1.svg48180 × 33
12 × 34
0 × 35
6 × 36		Oh, [4,3]
8Polyiamond-4-3.svg126

Non-convex forms

There are an infinite number of nonconvex forms.

Some examples of face-intersecting deltahedra:

  • Great icosahedron - a Kepler-Poinsot solid, with 20 intersecting triangles [[INLINE_IMAGE|//upload.wikimedia.org/wikipedia/commons/thumb/e/eb/Great_icosahedron.png/160px-Great_icosahedron.png|//upload.wikimedia.org/wikipedia/commons/thumb/e/eb/Great_icosahedron.png/240px-Great_icosahedron.png 1.5x, //upload.wikimedia.org/wikipedia/commons/thumb/e/eb/Great_icosahedron.png/320px-Great_icosahedron.png 2x|Great icosahedron.png|h168|w160]]

Other nonconvex deltahedra can be generated by adding equilateral pyramids to the faces of all 5 regular polyhedra:

5-cell net.pngPyramid augmented cube.pngStella octangula.pngPyramid augmented dodecahedron.pngTetrahedra augmented icosahedron.png
triakis tetrahedrontetrakis hexahedrontriakis octahedron
(stella octangula)		pentakis dodecahedrontriakis icosahedron
12 triangles24 triangles60 triangles

Other augmentations of the tetrahedron include:

Examples: Augmented tetrahedra
Biaugmented tetrahedron.pngTriaugmented tetrahedron.pngQuadaugmented tetrahedron.png
8 triangles10 triangles12 triangles

Also by adding inverted pyramids to faces:

  • Excavated dodecahedron

Third stellation of icosahedron.png
Excavated dodecahedron		Toroidal polyhedron.gif
A toroidal deltahedron
60 triangles48 triangles

See also

  • Simplicial polytope - polytopes with all simplex facets

References

[1]
Citation Linkopenlibrary.orgFreudenthal, H; van der Waerden, B. L. (1947), "Over een bewering van Euclides ("On an Assertion of Euclid")", Simon Stevin (in Dutch), 25: 115–128 (They showed that there are just 8 convex deltahedra. )
Sep 29, 2019, 10:12 AM
[2]
Citation Link//www.jstor.org/stable/2689647Trigg, Charles W. (1978), "An Infinite Class of Deltahedra", Mathematics Magazine, 51 (1): 55–57, JSTOR 2689647.
Sep 29, 2019, 10:12 AM
[3]
Citation Linkwww.interocitors.comThe Convex Deltahedra And the Allowance of Coplanar Faces
Sep 29, 2019, 10:12 AM
[4]
Citation Linkmathworld.wolfram.com"Deltahedron"
Sep 29, 2019, 10:12 AM
[5]
Citation Linkweb.archive.orgThe eight convex deltahedra
Sep 29, 2019, 10:12 AM
[6]
Citation Linkweb.archive.orgDeltahedron
Sep 29, 2019, 10:12 AM
[7]
Citation Linkweb.archive.orgDeltahedron
Sep 29, 2019, 10:12 AM
[8]
Citation Linkwww.jstor.org2689647
Sep 29, 2019, 10:12 AM
[9]
Citation Linkwww.interocitors.comThe Convex Deltahedra And the Allowance of Coplanar Faces
Sep 29, 2019, 10:12 AM
[10]
Citation Linkmathworld.wolfram.com"Deltahedron"
Sep 29, 2019, 10:12 AM
[11]
Citation Linkweb.archive.orgThe eight convex deltahedra
Sep 29, 2019, 10:12 AM
[12]
Citation Linkweb.archive.orgDeltahedron
Sep 29, 2019, 10:12 AM
[13]
Citation Linkweb.archive.orgDeltahedron
Sep 29, 2019, 10:12 AM
[14]
Citation Linken.wikipedia.orgThe original version of this page is from Wikipedia, you can edit the page right here on Everipedia.Text is available under the Creative Commons Attribution-ShareAlike License.Additional terms may apply.See everipedia.org/everipedia-termsfor further details.Images/media credited individually (click the icon for details).
Sep 29, 2019, 10:12 AM