Cubic crystal system

Cubic crystal system
There are three main varieties of these crystals:
Each is subdivided into other variants listed below. Note that although the unit cell in these crystals is conventionally taken to be a cube, the primitive unit cell often is not.
Bravais lattices
The three Bravais lattices in the cubic crystal system are:
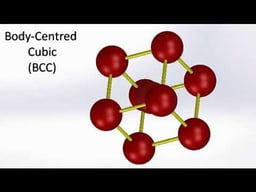
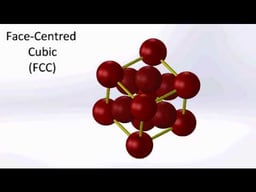
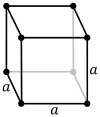
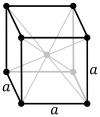
The primitive cubic system (cP) consists of one lattice point on each corner of the cube. Each atom at a lattice point is then shared equally between eight adjacent cubes, and the unit cell therefore contains in total one atom (1⁄8 × 8).The body-centered cubic system (cI) has one lattice point in the center of the unit cell in addition to the eight corner points. It has a net total of 2 lattice points per unit cell (1⁄8 × 8 + 1).The face-centered cubic system (cF) has lattice points on the faces of the cube, that each gives exactly one half contribution, in addition to the corner lattice points, giving a total of 4 lattice points per unit cell (1⁄8 × 8 from the corners plus 1⁄2 × 6 from the faces). Each sphere in a cF lattice has coordination number 12. Coordination number is the number of nearest neighbours of a central atom in the structure.
The face-centered cubic system is closely related to the hexagonal close packed (hcp) system, where two systems differ only in the relative placements of their hexagonal layers. The [111] plane of a face-centered cubic system is a hexagonal grid.
Attempting to create a C-centered cubic crystal system (i.e., putting an extra lattice point in the center of each horizontal face) would result in a simple tetragonal Bravais lattice.
Crystal classes
The isometric crystal system class names, point groups (in Schönflies notation, Hermann–Mauguin notation, orbifold, and Coxeter notation), type, examples, International Tables for Crystallography space group number,[2] and space groups are listed in the table below. There are a total 36 cubic space groups.
| Point group | Type | Example | Space groups | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Name[3] | Schön. | Intl | Orb. | Cox. | Primitive | Face-centered | Body-centered | |||
| 195–197 | Tetartoidal | T | 23 | 332 | [3,3] | enantiomorphic | Ullmannite, Sodium chlorate | P23 | F23 | I23 |
| 198–199 | P213 | I213 | ||||||||
| 200–204 | Diploidal | Th | 2/m3 (m3) | 3*2 | [3 | centrosymmetric | Pyrite | Pm3, Pn3 | Fm3, Fd3 | I3 |
| 205–206 | Pa3 | Ia3 | ||||||||
| 207–211 | Gyroidal | O | 432 | 432 | [3,4] | enantiomorphic | Petzite | P432, P4232 | F432, F4132 | I432 |
| 212–214 | P4332, P4132 | I4132 | ||||||||
| 215–217 | Hextetrahedral | Td | 43m | *332 | [3,3] | Sphalerite | P43m | F43m | I43m | |
| 218–220 | P43n | F43c | I43d | |||||||
| 221–230 | Hexoctahedral | Oh | 4/m32/m (m3m) | *432 | [3,4] | centrosymmetric | Galena, Halite | Pm3m, Pn3n, Pm3n, Pn3m | Fm3m, Fm3c, Fd3m, Fd3c | Im3m, Ia3d |
Other terms for hexoctahedral are: normal class, holohedral, ditesseral central class, galena type.
Voids in the unit cell
A simple cubic unit cell has a single cubic void in the center.
A body-centered cubic unit cell has six octahedral voids located at the center of each face of the unit cell, and twelve further ones located at the midpoint of each edge of the same cell, for a total of six net octahedral voids. Additionally, there are 24 tetrahedral voids located in a square spacing around each octahedral void, for a total of twelve net tetrahedral voids. These tetrahedral voids are not local maxima and are not technically voids, but they do occasionally appear in multi-atom unit cells.
A face-centered cubic unit cell has eight tetrahedral voids located midway between each corner and the center of the unit cell, for a total of eight net tetrahedral voids. Additionally, there are twelve octahedral voids located at the midpoints of the edges of the unit cell as well as one octahedral hole in the very center of the cell, for a total of four net octahedral voids.
One important characteristic of a crystalline structure is its atomic packing factor. This is calculated by assuming that all the atoms are identical spheres, with a radius large enough that each sphere abuts on the next. The atomic packing factor is the proportion of space filled by these spheres.
Assuming one atom per lattice point, in a primitive cubic lattice with cube side length a, the sphere radius would be a⁄2 and the atomic packing factor turns out to be about 0.524 (which is quite low). Similarly, in a bcc lattice, the atomic packing factor is 0.680, and in fcc it is 0.740. The fcc value is the highest theoretically possible value for any lattice, although there are other lattices which also achieve the same value, such as hexagonal close packed (hcp) and one version of tetrahedral bcc.
As a rule, since atoms in a solid attract each other, the more tightly packed arrangements of atoms tend to be more common. (Loosely packed arrangements do occur, though, for example if the orbital hybridization demands certain bond angles.) Accordingly, the primitive cubic structure, with especially low atomic packing factor, is rare in nature, but is found in polonium.[4][5] The bcc and fcc, with their higher densities, are both quite common in nature. Examples of bcc include iron, chromium, tungsten, and niobium. Examples of fcc include aluminium, copper, gold and silver.
Multi-element compounds
Compounds that consist of more than one element (e.g. binary compounds) often have crystal structures based on a cubic crystal system. Some of the more common ones are listed here.
Caesium chloride structure
The space group of the caesium chloride (CsCl) structure is called Pm3m (in Hermann–Mauguin notation), or "221" (in the International Tables for Crystallography). The Strukturbericht designation is "B2".[6]
One structure is the "interpenetrating primitive cubic" structure, also called the "caesium chloride" structure. Each of the two atom types forms a separate primitive cubic lattice, with an atom of one type at the center of each cube of the other type. Altogether, the arrangement of atoms is the same as body-centered cubic, but with alternating types of atoms at the different lattice sites (see picture here [19] ). Alternately, one could view this lattice as a simple cubic structure with a secondary atom in its cubic void.
In addition to caesium chloride itself, the structure also appears in certain other alkali halides when prepared at low temperatures or high pressures.[7] Generally, this structure is more likely to be formed from two elements whose ions are of roughly the same size (for example, ionic radius of Cs+ = 167 pm, and Cl− = 181 pm).
The coordination number of each atom in the structure is 8: the central cation is coordinated to 8 anions on the corners of a cube as shown, and similarly, the central anion is coordinated to 8 cations on the corners of a cube.
Other compounds showing caesium chloride like structure are CsBr, CsI, high-temp RbCl, AlCo, AgZn, BeCu, MgCe, RuAl and SrTl.
Rock-salt structure
The space group of the rock-salt (NaCl) structure is called Fm3m (in Hermann–Mauguin notation), or "225" (in the International Tables for Crystallography). The Strukturbericht designation is "B1".[8]
In the rock-salt or sodium chloride (halite) structure, each of the two atom types forms a separate face-centered cubic lattice, with the two lattices interpenetrating so as to form a 3D checkerboard pattern. Alternately, one could view this structure as a face-centered cubic structure with secondary atoms in its octahedral holes.
Examples of compounds with this structure include sodium chloride itself, along with almost all other alkali halides, and "many divalent metal oxides, sulfides, selenides, and tellurides".[7] More generally, this structure is more likely to be formed if the cation is somewhat smaller than the anion (a cation/anion radius ratio of 0.414 to 0.732).
The coordination number of each atom in this structure is 6: each cation is coordinated to 6 anions at the vertices of an octahedron, and similarly, each anion is coordinated to 6 cations at the vertices of an octahedron.
Zincblende structure
The Zincblende structure (also written "zinc blende") is named after the mineral zincblende (sphalerite), one form of zinc sulfide (β-ZnS). As in the rock-salt structure, the two atom types form two interpenetrating face-centered cubic lattices. However, it differs from rock-salt structure in how the two lattices are positioned relative to one another. The zincblende structure has tetrahedral coordination: Each atom's nearest neighbors consist of four atoms of the opposite type, positioned like the four vertices of a regular tetrahedron. Altogether, the arrangement of atoms in zincblende structure is the same as diamond cubic structure, but with alternating types of atoms at the different lattice sites.
Examples of compounds with this structure include zincblende itself, lead(II) nitrate, many compound semiconductors (such as gallium arsenide and cadmium telluride), and a wide array of other binary compounds.
Other compounds showing zinc blende-like structure are α-AgI, β-BN, diamond, CuBr, β-CdS, BP and BAs.
Weaire–Phelan structure
The Weaire–Phelan structure has Pm3n (223) symmetry.
It has 3 orientations of stacked tetradecahedrons with pyritohedral cells in the gaps. It is found as a crystal structure in chemistry where it is usually known as the "Type I clathrate structure". Gas hydrates formed by methane, propane, and carbon dioxide at low temperatures have a structure in which water molecules lie at the nodes of the Weaire–Phelan structure and are hydrogen bonded together, and the larger gas molecules are trapped in the polyhedral cages.
See also
Atomium: building which is a model of a bcc unit cell, with vertical body diagonal.
Dislocations
Reciprocal lattice